Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#1 08-03-2021 11:57:50
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 989
Connaissez-vous les figures de Paul Schatz dont l'oloïde ?
Salut jeunesse,
Durant mon absence déménageuse, un de mes beaux-frères m'a fait découvrir un solide nommé "oloïde" ("inventé" par un certain Paul Schatz), qui ressemble à une moule...
Suite à la suggestion de wiwaxia, j'en fait une discussion à part.
En fait, mon beau-frère, m'a aussi montré (réalisé en carton), un découpage du cube dit "cube inversible" de Paul Shatz, ceci expliquait la place de mon post : vous auriez tôt ou tard découvert ce cube
https://www.youtube.com/watch?v=WNbcy5qAwHE
Ses équations (et plus encore) sont sur https://mathcurve.com/surfaces/orthobic … ycle.shtml
Après vous être bien amusés avec les cubes (et variantes) si vous ne connaissiez pas, vous devriez aimer...
En fait, mon beau-frère, m'a aussi montré (réalisé en carton), un découpage du cube dit "cube inversible" de Paul Shatz, ceci expliquait la place de mon post : vous auriez tôt ou tard découvert ce cube.
Liens videos :
https://www.youtube.com/watch?v=uAJE9Z1Jr64 rotations en kaléidoscope du cube découpé...
https://www.youtube.com/watch?v=1f3QfWRI-C8 construction du cube en 3D avec Sketchup (doit pouvoir se faire avec GG)
Et je trouve qu'il y a aussi une parenté (+ ou - lointaine certes) avec le sujet traité par wiwaxia sur le découpage du cube en tétraèdres...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#2 08-03-2021 20:33:12
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Connaissez-vous les figures de Paul Schatz dont l'oloïde ?
Bonjour,
L'objet est en effet remarquable, tant par sa forme que par son mouvement de roulement.
La comparaison des mouvements (filmés à partir de 4 min 25) n'est cependant guère convaincante: il eût fallu pour cela lancer une sphère ou un cylindre métallique de dimensions et de densité comparables, et non un rouleau de ruban adhésif beaucoup plus léger.
Et la justification donnée plus loin (4:40 à 4:50) l'est encore moins:
À chaque demi-rotation il va bénéficier d'une nouvelle petite poussée, un nouveau petit élan si vous voulez ...
Le barycentre reste à distance fixe de l'objet (la ligne de roulement demeurant tangente à la sphère inscrite, si j'ai bien vu), et il se déplace horizontalement d'un mouvement théoriquement uniforme, de fait légèrement décéléré à cause des frottements.
On le voit même un bref instant repartir en sens opposé en fin de course (5:26), ce qui laisses quelques doutes sur l'horizontalité du sol ...
Le sujet abordé est aussi intéressant qu'inattendu.
On trouve quelques liens sur Wikipédia
https://fr.wikipedia.org/wiki/Olo%C3%AFde
Je n'ai rien compris à l'équation cartésienne, polynôme comportant 48 termes mais aucune constante: l'origine (0,0,0) vérifie apparemment l'équation; la somme paraît dépourvue de toute symétrie interne apparente.
... Et je trouve qu'il y a aussi une parenté (+ ou - lointaine certes) avec le sujet traité par wiwaxia sur le découpage du cube en tétraèdres ...
Tout à fait. Le découpage conduit ici à un enchaînement cyclique et flexible de 6 tétraèdres allongés.

Il faudrait pointer certains sommets sur une série de constructions intermédiaires pour mettre en évidence l'inversion.
PS: Pas étonnante, l'absence de symétrie: l'origine est au centre du cercle horizontal !
Dernière modification par Wiwaxia (09-03-2021 00:44:11)
Hors ligne
#3 08-03-2021 22:29:08
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Connaissez-vous les figures de Paul Schatz dont l'oloïde ?
Bonsoir !
ce cube me rappelle des choses ... et justement des tétraèdres.
Je dois refaire le dessin, mais il est possible de couper un tétraèdre en 4, et de l'ouvrir, comme les "flexo-machins" qu'on voit parfois.
Je vais revoir cela demain ...
Mais c'est très amusant !
Cordialement, B-m
PS : d'accord avec Wiwaxia sur l'inertie de l'objet oloïde ... sauf sur la position, que je pense être au milieu des 2 centres de cercles ...?
Dernière modification par Bernard-maths (08-03-2021 22:32:22)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#4 09-03-2021 22:44:27
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Connaissez-vous les figures de Paul Schatz dont l'oloïde ?
Bonsoir !
J'ai pas beaucoup de temps en ce moment ...
MON tétraèdre n'est pas génial, il s'articule seulement selon 2 arêtes, l'une ou l'autre, mais pas les 2, beuhhh.
DONC je cours après 2 lièvres (Wiwaxia connaît bien), l'un à décomposer un octaèdre, "façon cube de Schatz", et l'autre à la place des cercles de l'oloïde, mettre des polygones. Donc obtenir des "polygonoïdes" ... ?
Allez, bonne soirée,
Bernard-maths
Dernière modification par Bernard-maths (09-03-2021 22:45:11)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#5 10-03-2021 10:07:45
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Connaissez-vous les figures de Paul Schatz dont l'oloïde ?
Bonjour,
... DONC je cours après 2 lièvres (Wiwaxia connaît bien), l'un à décomposer un octaèdre, "façon cube de Schatz", et l'autre à la place des cercles de l'oloïde, mettre des polygones. Donc obtenir des "polygonoïdes" ... ?
Mon lumbago, qui me rappelle très inopportunément mon état-civil, ne m'autorise pas à me prendre pour un lièvre et encore moins à pratiquer le tennis ou le basket, activités où la balle présente un axe de roto-inversion d'ordre 4 - à l'instar de l'oloÏde et du sphéricône.
Le polygonoïde que tu évoques est un dodécaèdre résultant de la déformation d'un cube, et du pliage selon une diagonale des 6 faces carrées, l'un des axes de symétrie d'ordre (4) se transformant en axe de roto-inversion.
https://mathcurve.com/courbes3d/couture/couture.shtml
http://images.math.cnrs.fr/La-balle-et-la-courbe.html
https://www.freepng.fr/png-igho28/
http://cge2016.impmc.upmc.fr/ppt/Garreau.pdf
https://coursgeologie.com/les-operation … metrie-244
Dernière modification par Wiwaxia (10-03-2021 11:37:47)
Hors ligne
#6 10-03-2021 10:22:45
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Connaissez-vous les figures de Paul Schatz dont l'oloïde ?
Hello !
Oui, je me suis rendu compte qu'on pouvait tirer sur un octaèdre et le déformer ainsi ...
Et puis à 3h20 cette nuit, j'ai pensé qu'il vaudrait mieux les appeler des polygonoèdres, et non oïdes ... ?
Je crois que je vais retourner à mes préparations pour la quinzaine de "Maths en Scène" à Montpellier !
J'ai une activité de cube retournable, qui amuse beaucoup les "petits" primaire ou collège ... Je vais la faire passer ... ce soir ?
Bonne journée, B-m
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#7 10-03-2021 11:15:06
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Connaissez-vous les figures de Paul Schatz dont l'oloïde ?
Voici les liens
https://cjoint.com/c/KCkjlFlHQaG
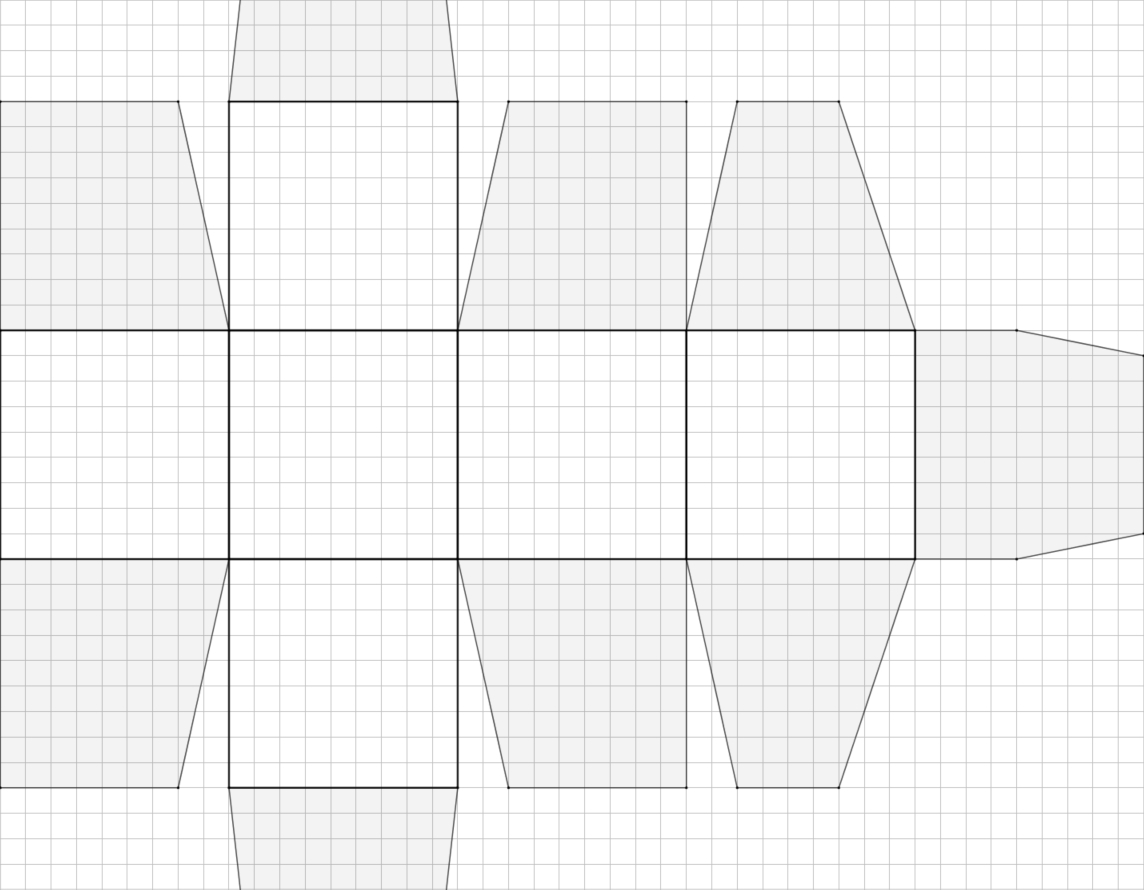
A imprimer format A4, et découper, plier dans les 2 sens. Les parties grises servent à bloquer le cube en position. Les autres pour la décoration ...
B-m
PS : hum, ça devient un peu poubelle ?
Dernière modification par Bernard-maths (10-03-2021 11:34:15)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#8 10-03-2021 11:35:31
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Connaissez-vous les figures de Paul Schatz dont l'oloïde ?
La figure résulte d'un dessin rapide - j'espère qu'elle montre la transformation du polyèdre, et la parenté de symétrie.


Hors ligne
#9 10-03-2021 16:36:58
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Connaissez-vous les figures de Paul Schatz dont l'oloïde ?
Suite de notre rubrique conchyliophile: le tracé "à main levée" des polyèdres d'ordre N = 3, 4 et 5 :

Pour N = 2 on obtient un tétraèdre déformé, pour N = 3 un octaèdre.
Il y a plus généralement S = 2N sommets, F = (4N - 4) faces et A = (6N - 6) arêtes.
La relation d'Euler S + F = A + 2 est vérifiée.
Dernière modification par Wiwaxia (12-03-2021 12:54:58)
Hors ligne
#10 18-03-2021 19:51:44
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Connaissez-vous les figures de Paul Schatz dont l'oloïde ?
Bonsoir à tous !
Je vous avais parlé d'un patron pour le cube de Paul Schatz, vous trouverez quelques pistes dans le document à charger :
https://cjoint.com/doc/21_03/KCsrVprvoG … 03-18.docx
Cordialement, Bernard-maths
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne








