Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#2 19-04-2020 20:48:39
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : demonstration du volume de cylindre oblique
Bonsoir,
La hauteur d'un cylindre est un mot "normalisé", c'est la distance (notion mathématique) qui sépare les deux disques de base.
Qu'appelez-vous Longueur du Cylindre ?
Le volume du cylindre est bien $V = \pi r^2h$
Que le cylindre soit oblique ne change rien :
supposons votre cylindre oblique posé sur un sol plat et horizontal. Si je cherche sa hauteur, pour être concret, je me place sur l'un des points du cercle supérieur et je laisse pendre un fil à plomb : la hauteur est dans ce cas la longueur du segment de perpendiculaire partant de mon point jusqu'au sol...
Si vos remettez ça en cause, alors vours remettez aussi en cause le volume du cube "oblique", du cône oblique, de ma pyramide oblique et vous dites alors que des générations et des générations de mathématiciens racontent n'importe quoi !
Ce serait grave...
@+
Arx Tarpeia Capitoli proxima...
En ligne
#3 21-04-2020 00:15:54
- risinus94
- Membre
- Inscription : 19-04-2020
- Messages : 3
Re : demonstration du volume de cylindre oblique
bon soir comme tu l'as dit si on a 2 cylindre sur sol plat de meme diametre mai de longueur differente alors ils ont la meme hauteur mais reelement n'ont pas le memme volume car leur longueurs sont differentes (la longueur c la distance qui separe leurs bases).
pour la pyramide oblique je cherche encore la demonstration merci
Hors ligne
#4 21-04-2020 10:10:52
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : demonstration du volume de cylindre oblique
Bonjour,
Tu ne trouveras nulle part (1) la démonstration d'une formule fausse.
Pour te convaincre de ton erreur, tu peux reprendre l'analogie du cylindre oblique avec une pile de pièces de monnaie: elle est connue depuis quatre siècles ...
http://villemin.gerard.free.fr/GeomLAV/ … tm#oblique
Pour les pyramides et les cônes obliques, résultat semblable : V = (1/3)Sh ,
hormis l'intervention d'un facteur différent de l'unité.
http://villemin.gerard.free.fr/GeomLAV/ … tm#mesures
(1) sur tout site de mathématiques digne de ce nom, évidemment ...
Dernière modification par Wiwaxia (21-04-2020 10:28:49)
Hors ligne
#5 21-04-2020 11:43:40
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : demonstration du volume de cylindre oblique
Bonjour,
Dans ma réponse à côté du mot distance, j'avais écrit entre parenthèses notion mathématique...
Ta formulation n'est pas correcte
- si tu dis : la longueur, c'est la distance entre les centres, ok
- mais tu as dit : la distance entre les bases... La distance entre les bases parallèles c'est ce qu'on appelle hauteur : c'est la longueur du segment de perpendiculaire abaissée d'une base sur l'autre.
Si tu es logique dans ton raisonnement, alors
- tu dois nier l'égalité des aires entre le rectangle ABCD et le parallélogramme EFGH du dessin visible ici : https://www.cjoint.com/c/JDviseF6slW Oui/Non ?
- tu dois nier l'égalité des volumes entre lce prisme droit (parallélépipède rectangle) et prisme oblique : https://www.cjoint.com/c/JDvjOGbEjmW Oui/Non ?
si on a 2 cylindre sur sol plat de meme diametre mai de longueur differente alors ils ont la meme hauteur mais reelement n'ont pas le memme volume
Bien sûr que si !
C'est le mathématicien "italien" Bonaventura Cavalieri (1598 - 1647), donc un contemporain de... Henri IV (assassiné en 1610) qui le premier a montré cela pour quel quel solide.
J'adapte ce qu'il a montré au cas du cylindre oblique :
- puisque les 2 disques délimitant le cylindre sont parallèles et de même taille, alors tous les disques résultant de la coupe du cylindre oblique par un plan parallèle sont des disques superposables et donc de même aire,
- et donc dans ce cas le volume d'un cylindre droit et du cylindre oblique, de même hauteur ayant des disques de base de même taille sont égaux.
Tu penses vraiment que depuis 350 ans, aucun mathématicien ne s'est rendu compte qu'il avait raconté des sottises ?
Allons, allons ! Surtout que jusqu'au XIXe s, ils étaient tous à l'affût de que faisaient leurs confrères et essayaient d'améliorer voire de démolir ce qui avait été fait dans le passé, et ainsi laisser leur nom dans l'histoire...
Et entre tous les Physiciens, les Techniciens, les artisans de base qui font très souvent ce genre de calcul, personne n'a encore découvert l'erreur ?
@+
Arx Tarpeia Capitoli proxima...
En ligne
#6 21-04-2020 22:47:45
- risinus94
- Membre
- Inscription : 19-04-2020
- Messages : 3
Re : demonstration du volume de cylindre oblique
bon jour , voici ma demonstration :sur l'axe ox qui part du centre de la base inferieur e rejoint la base suerieure an a volume du cylindre oblique est egal a :
v=integral(entre 0 et L) pi*r2*dx=pi*r2*inegral(entre o et L)= pi*[x](entre 0 et L)= pi*r2*L
L:distance entre le centre o de la base inferieure det le centre de la base superieure.
s'il y a une ereur veuillez me la faire connaitre.
je tiens a te dire mon ami que je ne cherche que la verite de la chose , et je respecte bien le travail des mathematiciens et des savants auparavant qui ont servi l'humanite et propager de lumiere dans notre vie. merci bien.
Hors ligne
#7 22-04-2020 09:40:57
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : demonstration du volume de cylindre oblique
Bonjour,
Parce que tu sais jouer avec les intégrales ou tu as recopié et adapté une formule ?
$v=\int_ 0^L\pi r^2\; dx=\pi r^2\int_ 0^ L\;dx= \pi r^2 [x]_0^L= \pi r^2 L$
Et si moi, je remplace L par h ? Je trouve bien $\pi r^2 h$, alors ?
Je vois que tu cherches peut-être à faire connaître ta vérité, mais que tu as soigneusement évité de répondre aux questions que je t'ai posées... C'est bien dommage.
Parce que, comme je te l'ai dit, ta logique s'applique aussi (par exemple) aux prismes obliques :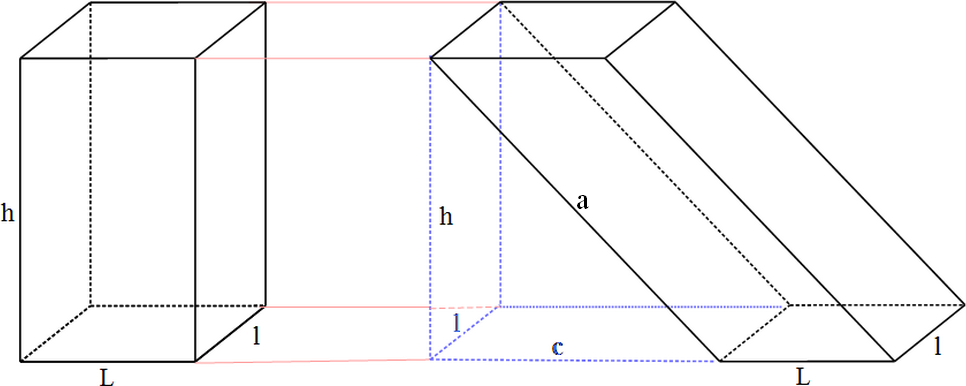
Les deux prismes, logiquement, ont pour toi les volumes :
$V_d = L\times l \times h$
$V_o = L\times l \times a$
Et avec ta démo, je montre comment on arrive à $V_o$ :
$\int_0^a L\times l\;dx=L\times l \int_0^a\, dx =L\times l \left[x\right]_0^a=L\times l\times a$
La formule est fausse et je le prouve sans intégrale...
Pour transformer le prisme oblique en un prisme droit de dimensions (L+c), l, h et de volume $V = (L+c)\times l \times h$
Je complète de chaque côté mon prisme oblique avec 2 prismes droits à base triangulaire (je n'en ai tracé qu'un (en bleu et en pointillés)
Chaque prisme bleu a pour aire de base l'aire du triangle rectangle de côtés c et h, soit $\dfrac{c \times h}{2}$ et de hauteur l.
Volume total des deux prismes bleu : $ 2 \times \dfrac{c \times h}{2} \times l =c\times h \times l$
Au prisme droit complété de volume $(L+c)\times l\times h$ j'enlève le volume total des deux bleus, je trouve bien les volume du prisme oblique noir :
$V_o=(L+c)\times l \times h - c\times h \times l = (L \times l \times h + c \times l \times h)-c\times h \times l$
$\quad\;=L \times l \times h+ c \times l \times h - c\times h \times l= L \times l \times h$
Alors ?
Alors ta méthode ne marche pas : l'erreur n'est pas une erreur de calcul mais une faute technique...
Réfléchis bien sur l'emploi de l'intégrale par moi et par toi : l'une est juste, l'autre est fausse.
Cherche pourquoi !
Si tu ne trouves pas, je le dirai en 1 ligne...
@+
Arx Tarpeia Capitoli proxima...
En ligne
#8 19-03-2023 19:44:26
- Becker
- Invité
Re : demonstration du volume de cylindre oblique
L'élément de volume dV=produit scalaire du vecteur S (de module constant = πr²) avec le vecteur dl, lequel est orienté selon la ligne directrice du cylindre oblique
dV= S.dl.cos (ɑ) [ɑ = angle entre la verticale et la ligne directrice du cylindre oblique)
V= πr².cos (ɑ).∫dl (intégrale prise entre 0 et L)
On obtient bien, avec H = projection de L sur l'axe vertical:
V= πr².cos (ɑ). L = πr².H
#9 22-04-2023 22:40:38
- Zebulor
- Membre expert
- Inscription : 21-10-2018
- Messages : 2 089
Re : demonstration du volume de cylindre oblique
Bonsoir,
yoshi et Wiwaxia ont raison, j'ai trouvé à ce sujet un exercice dans abc du bac année 1990 aux editions nathan dont la correction est basée sur les homothéties.
Dernière modification par Zebulor (22-04-2023 22:41:38)
En matière d'intégrales impropres les intégrales les plus sales sont les plus instructives.
Hors ligne








