Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#1 04-05-2021 11:45:40
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Courbes et surfaces de niveaux ... et troncatures.
Bonjour à tous !
Bonjour à Wiwaxia, qui m'a "obligé" à ouvrir cette discussion ... :-)))
Après avoir parlé des équations de polyèdres (Voir : "La réduction des polyèdres convexes à l'intersection de demi-espaces"), je vais vous parler de 2 applications sur ces polyèdres (et peut-être d'autres).
La première concerne les courbes (en 2D) et les surfaces (en 3D) des polygones ou polyèdres, qui consiste, pour imager, à les faire grossir en dehors de l'objet de départ.
La deuxième concerne les troncatures, consistant à "découper" l'objet selon quelques "consignes".
Les deux activités peuvent être mises en relation, dans certains cas (pas tous !), d'où la même discussion ...
1er Principe utilisé : partir d'une équation de volume plein, et ajouter une constante pour obtenir des équations de surfaces, ou faire diminuer l'équation de volume et générer une équation de surface, qui simulera une troncature !
Nous sommes le 10 décembre, 7 mois plus tard ! J'ai entre-temps mis au point une autre technique de courbe ou surface de niveau, je vais donc la rajouter, et donner des exemples à partr de la discussion #24 ...
2ème principe utilisable : prendre une équation sous forme nulle, la mettre en valeur absolue et lui donner une valeur > 0 !
A bientôt, Bernard-maths
Dernière modification par Bernard-maths (10-12-2021 18:23:08)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#2 05-05-2021 14:41:00
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour à tous !
Je commence en 2D un 1er exemple de courbe de niveau, et de troncature : avec un rectangle.
Je commence par un rectangle ABCD, dans le plan (xOy) de l’espace. A(a,b),a=4, b=3, ici.
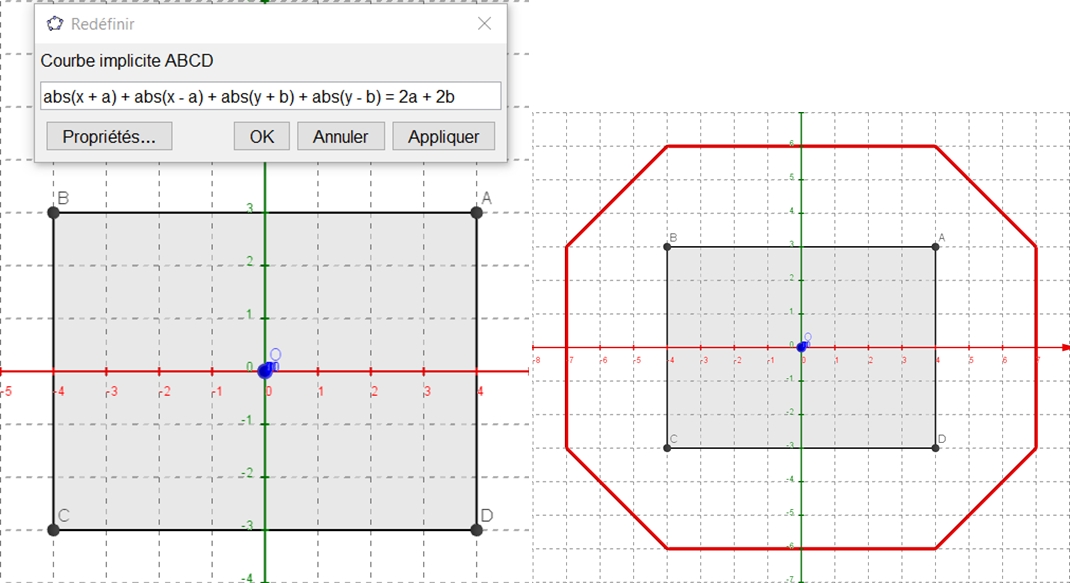
L’équation du rectangle plein s’obtient en tant qu’intersection des 2 bandes de plan comprises, l’une entre x=-a et x=a, l’autre entre y=-b et y=b. Les 2 membres de l’équation : abs(x + a) + abs(x - a) + abs(y + b) + abs(y - b) = 2a + 2b sont positifs, et elle exprime que tout point M dans le rectangle (bords compris) est à une somme constante des 4 distances aux 4 (supports des) côtés, et égale à 2a+2b. 2a+2b est le minimum !
Peut-on avoir plus que 2a+2b ? Soit e1 un nombre positif, alors l’ensemble des points M du plan vérifiant :
abs(x + a) + abs(x - a) + abs(y + b) + abs(y - b) = 2a + 2b + 2e1, est la courbe rouge, ici e1=3.
Cette courbe voit ses 4 côtés parallèles à ABCD de mêmes longueurs et à la distance e1 … et ses 4 côtés obliques « inclinés » à 45°.
Si e1=0, on retrouve l’équation de ABCD, et à mesure que e1 augmente, la courbe rouge se développe, en gardant 4 côtés parallèles et isométriques aux 4 côtés de ABCD, reliés par des côtés obliques « inclinés » à 45°.
Personnellement, je dis que la courbe rouge est « de niveau e1 par rapport à ABCD ».
Maintenant parlons troncature : cela revient, dans le plan, à couper les coins plus ou moins, et disons à 45° !
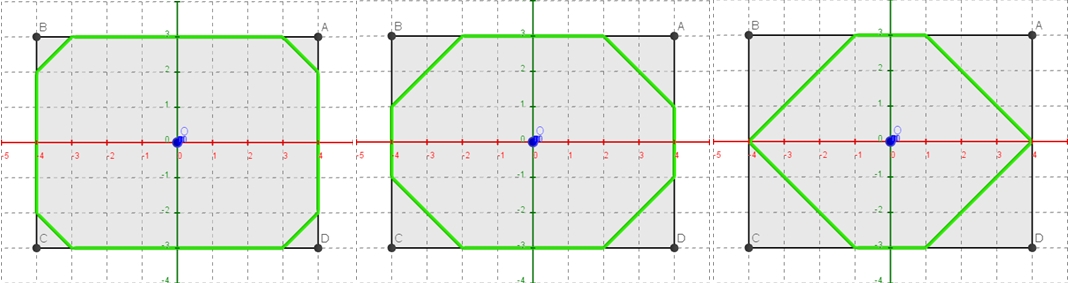
Les 3 images illustrent le procédé : en vert, on coupe les coins de plus en plus (on parle de troncature « légère » à « sévère »), tout en gardant le contact avec chacun des 4 bords : 3ème cas, où il ne reste qu’un point de contact à gauche et à droite. STOP !
On peut remarquer alors que les courbes vertes ressemblent aux rouges … mais à l’intérieur, au lieu de l’extérieur.
ON (moi, par exemple) peut alors penser à générer ces courbes vertes à partir d’un rectangle intérieur plus petit …
Dont acte : abs(x + a - k) + abs(x - a + k) + abs(y + b - k) + abs(y - b + k) = 2a + 2b - 4k, pour un rectangle intérieur bleu.
Où k est un paramètre permettant de réduire la taille de ABCD ; puis l’équation de la courbe verte s’écrit :
abs(x + a - k) + abs(x - a + k) + abs(y + b - k) + abs(y - b + k) = 2a + 2b - 4k + 2e2,
où e2 permet de générer une courbe de niveau par rapport au rectangle bleu ! Bien sur, ici, on prend e2 = k …
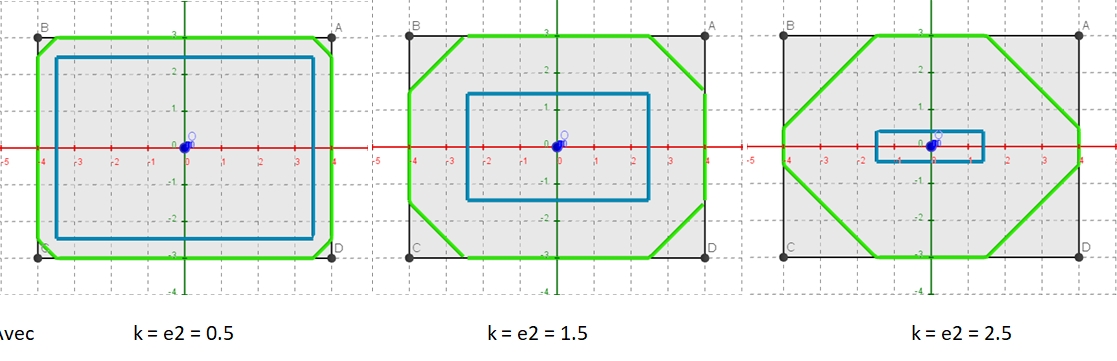
On peut donc simplifier l’équation de la courbe verte de troncature de ABCD, en remplaçant e2 par k :
abs(x + a - k) + abs(x - a + k) + abs(y + b - k) + abs(y - b + k) = 2a + 2b - 4k + 2e2 = 2a + 2b – 2k !!!
soit : abs(x + a - k) + abs(x - a + k) + abs(y + b - k) + abs(y - b + k) = 2a + 2b - 2k.
Conclusion : on vient de voir comment générer une courbe de niveau autour d’un rectangle, en fonction d’un paramètre.
Puis de générer une courbe de troncature de ce même rectangle, à partir d’une courbe de niveau associée …
EXERCICE, pour vous amuser ... On pose b = a = 4. ABCD est alors un carré.
1°) Pour quelle valeur de e2 a-t-on une courbe de niveau rouge en octogone régulier ?
2°) Pour quelle valeur de k a-t-on une troncature verte en octogone régulier ?
3°) Pour quelle valeur de k a-t-on une troncature sévère (et maximale) donnant le carré dual (intérieur) de ABCD ?
Pour chacune de ces 3 questions, vous pouvez donner l'équation correspondante, et même la vérifier pour un côté // aux axes, et pour un côté "oblique", compte tenu des symétries, ça doit aller partout ...
Voilà, bon courage, et à bientôt pour la 3D !
NB : si vous voulez des précisions, n'hésitez pas à demander.
Bernard-maths
Dernière modification par Bernard-maths (05-05-2021 14:59:45)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#3 05-05-2021 21:16:20
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonsoir à tous !
Mon ordi a planté, et j'ai perdu 1h de travail ! M'enfin ?
Bon, je vais vous commencer les surfaces de niveaux en 3D. J’agrandis la figure, en passant du rectangle ABCD à un parallélépipède rectangle ABCDEFGH, appelé l’objet ! (dans la suite).
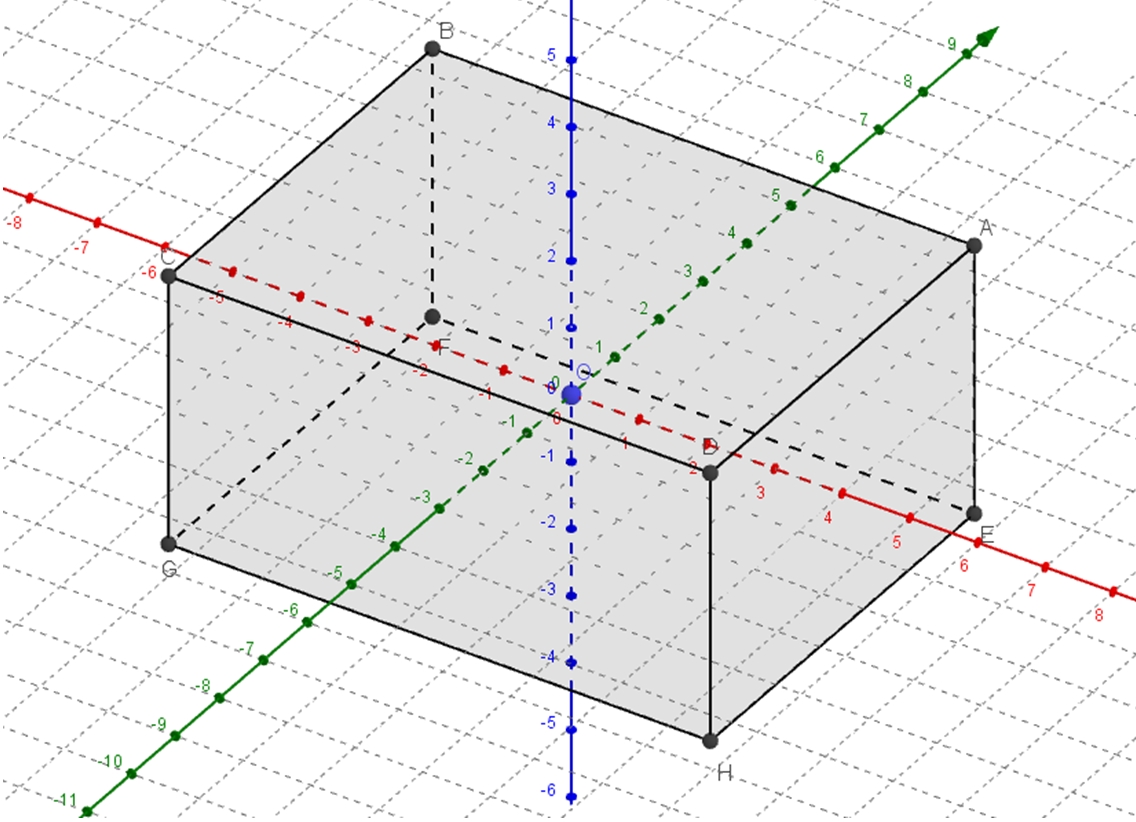
Avec A(a,b,c)=(4,3,2) ici. Il est à l’intersection de 3 tranches d’espace, la 1ère entre x=-a=-4 et x=a=4, la 2ème entre y=-b=-3 et y=b=3, et la 3ème entre z=-c=-2 et z=c=2. Son équation de volume plein est alors :
abs(x + a) + abs(x - a) + abs(y + b) + abs(y - b) + abs(z + c) + abs(z - c) = 2a + 2b + 2c.
Peut-on avoir plus que 2a+2b+2c ? Soit e1 un nombre réel positif, cherchons les points de l’espace tels que :
abs(x + a) + abs(x - a) + abs(y + b) + abs(y - b) + abs(z + c) + abs(z - c) = 2a + 2b + 2c + 2e1 !.
Eh bien, on trouve, comme pour le rectangle, une enveloppe extérieure (rouge) avec 6 faces rectangles parallèles aux 6 faces de l’objet, 12 autres rectangles parallèles aux 12 arêtes de l’objet, et 8 faces en triangles sur les 8 coins …
On aperçoit au travers l’objet. Cette surface possède donc 6 + 12 + 8 = 26 faces …
Comme pour le rectangle ABCD en 2D, si e1 augmente indéfiniment, les 6 faces parallèles à celles de l’objet, vont rester parallèles à distances e1 et isométriques, alors que les autres faces vont grandir indéfiniment !
Remarque : compte tenu des diverses symétries, il suffit de vérifier pour une face, une arête et un sommet/coin, que les équations des facettes sont bien données par l’équation générale ! Si quelqu’un en veut … ?
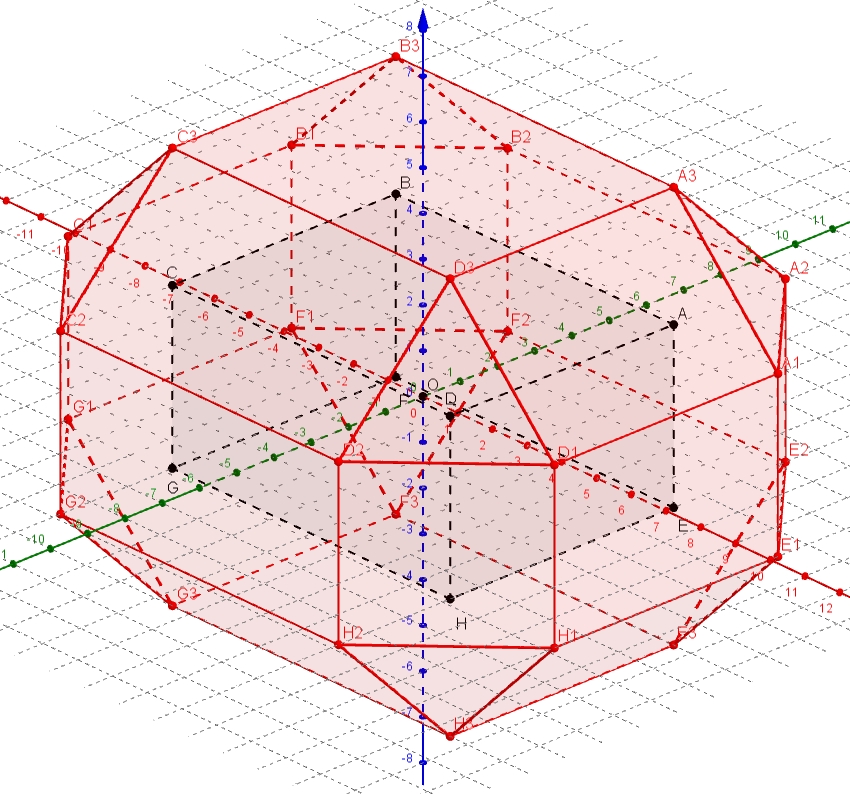
Exercice : si on égalise a=b=c=4, alors l'objet est un cube. Pouvez-vous déterminer pour quelle valeur de e1 tous les rectangles deviennent des carrés ? On a alors un rhombicuboctaèdre ... (régulier ?).
Voici les lien pour charge le fichier GeoGebra ... si ça marche ...
https://cjoint.com/c/KEftBLSxm6f
https://cjoint.com/doc/21_05/KEftBLSxm6 … -05-05.ggb
Bonne soirée, Bernard-maths
Dernière modification par Bernard-maths (05-05-2021 21:29:58)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#4 06-05-2021 21:31:29
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonsoir à tous !
Alors ? Passons maintenant à la troncature : pour un polyèdre, il s’agit de couper parallèlement aux arêtes (disons à 45°), et les sommets/coins en triangles équilatéraux. Légèrement à sévèrement ! S’arrêter lorsqu’on n’a plus qu’un point ou un segment de contact avec une des 6 faces de l’objet …
Ici aussi, on va définir un parallélépipède rectangle, réduction de l’objet, selon un paramètre k, puis définir une surface de niveau par rapport à cet objet interne, de façon qu’elle colle à l’objet initial par les faces parallèles.
L’objet a les mêmes dimensions qu’avant A(a,b,c)=(4,3,2). Mais maintenant nous définissons un polyèdre A0B0C0D0E0F0G0H0 interne, en réduisant selon le paramètre k. Ainsi A0(a-k,b-k,c-k), donc si k=1, alors A0(3,2,1) …
Son équation de volume plein est donc :
abs(x + a-k) + abs(x – a+k) + abs(y + b-k) + abs(y – b+k) + abs(z + c-k) + abs(z – c+k) = 2a + 2b + 2c - 6k.
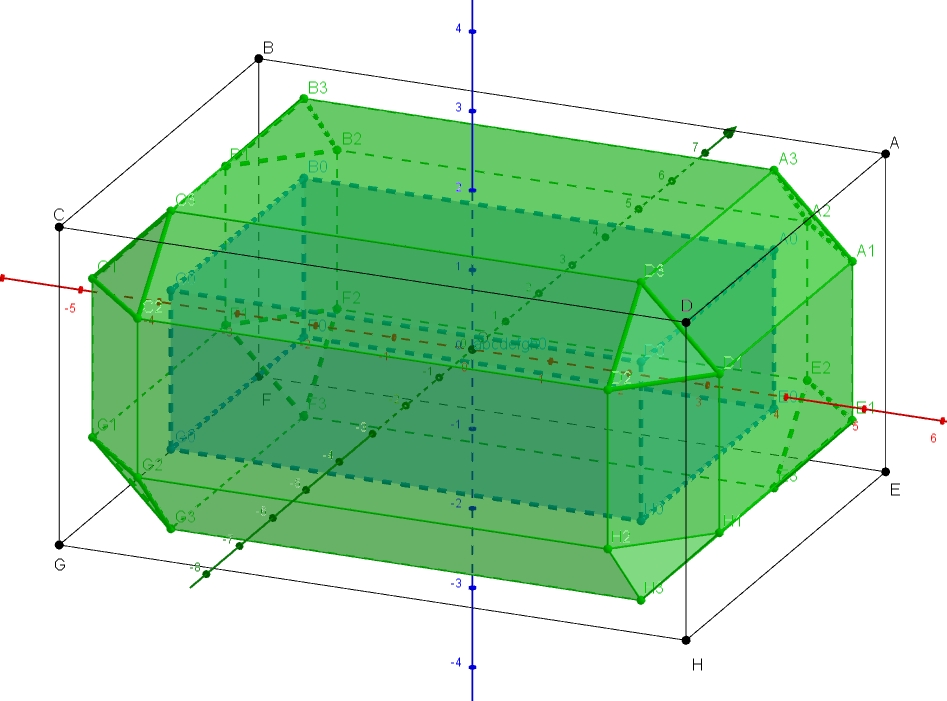
Et pour le programme GeoGebra :
https://cjoint.com/doc/21_05/KEgtJWZjO7 … -05-06.ggb
Et si on cherche la courbe de niveau « collée » à l’objet par les faces parallèles, il faut ajouter 2k … 2 fois l’écart.
Alors l’équation cherchée pour l’enveloppe verte est finalement :
abs(x + a-k) + abs(x – a+k) + abs(y + b-k) + abs(y – b+k) + abs(z + c-k) + abs(z – c+k) = 2a + 2b + 2c - 4k.
Vérification : je vous propose une vérification dans le cas présent, avec A(4,3,2) et A0(3,2,1). Donc retrouver les équations des 26 faces de la surface de niveaux verte.
Compte tenu des multiples symétries de la figure, il suffit de vérifier pour les 3 types de faces de celle-ci, à savoir : la face A1D1H1E1, à droite, la face oblique A1A3D3D1, à droite vers le haut, et la face triangulaire A1A2A3 vers le coin A !
Une démonstration serait similaire, mais avec les coordonnées variables des points …
Donc l’équation ici s’écrit : abs(x + 3) + abs(x – 3) + abs(y + 2) + abs(y – 2) + abs(z + 1) + abs(z – 1) = 14.
Pour A1D1H1E1, face à A0D0H0E0, on a : x ≥ 3, -2 ≤ y ≤ 2, et -1 ≤ z ≤ 1. Alors abs(x + 3) + abs(x – 3) = 2x ; abs(y + 2) + abs(y – 2) = 4 ; et abs(z + 1) + abs(z – 1) = 2. L’équation devient : 2x + 4 + 2 = 14, d’où x = 4 ! Equation du plan de la face.
C’est bien le cas de A1D1H1E1, pour lequel : x = 4 et -2 ≤ y ≤ 2, et -1 ≤ z ≤ 1.
Pour A1A3D3D1, en regard de l’arête [A0D0],on a : x ≥ 3, -2 ≤ y ≤ 2, et 1 ≤ z. Alors abs(x + 3) + abs(x – 3) = 2x ; abs(y + 2) + abs(y – 2) = 4 ; et abs(z + 1) + abs(z – 1) = 2z. L’équation devient : 2x + 4 + 2z = 14, d’où x + z = 5 !
C’est l’équation du plan contenant A1A3D3D1, et passant par les points d’abscisse x = 5 sur (x’x), et de cote z = 5 sur (z’z).
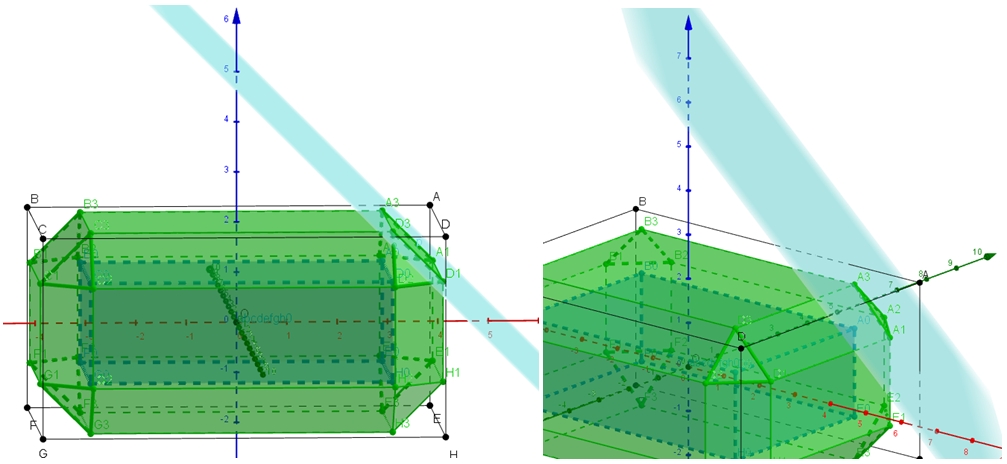
Enfin pour A1A2A3 : on a x ≥ 3, y ≥ 2 et z ≥ 1. L’équation … devient : 2x + 2 + 2z =14, soit x + y + z = 7.
C’est l’équation du plan contenant A1A2A3, et passant par les points d’abscisse x = 7 sur (x’x), d’ordonnée y = 7 sur (y’y), et de cote z = 7 sur (z’z).
Pour finir ce soir, un exercice :
Si on fait un cube avec a=b=c=4, pour quelle valeur de k la surface verte a-t-elle ses faces quadrilatères toutes carrées ? On a un rhombicuboctaèdre encore ...
Bernard-maths
Dernière modification par Bernard-maths (06-05-2021 21:48:26)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#5 07-05-2021 21:39:02
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonsoir à tous !
je passe à la suite ... Mais d’abord, corrigeons les exercices … en discussion #2, en prenant a=b=4 … en fait le curseur e1 étant limité à 5, on ne peut pas rendre la courbe de niveau rouge en octogone régulier … Je vous fais la figure pour a=b=3. Mais nous allons raisonner avec a et e1 d’une façon générale ! La figure de gauche est faite avec a=3 et e1=5.
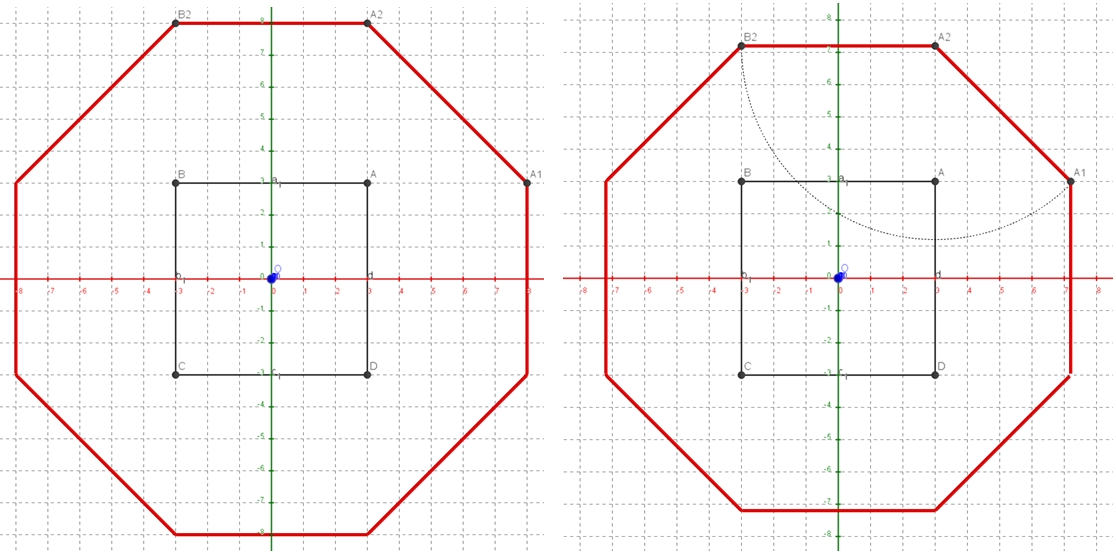
1°) Pour avoir un octogone régulier, il faut que A1A2 = A2B2. Or le triangle AA1A2 est rectangle isocèle de côté AA1 = e1, et A2B2 = 2a. Donc A1A2 = e1 √2 d’où l’équation : e1 √2 = 2a, et donc e1 = a √2. Sur la figure e1 = 3 √2 ≈ 4.2 -> figure droite.
Un arc de cercle en pointillés est tracé, de centre A2, et passant par B2 et A1 … pour vérifier visuellement.
2°) Pour avoir une troncature verte en octogone régulier, c’est pareil, il faut que A3A4 = A4B4 !
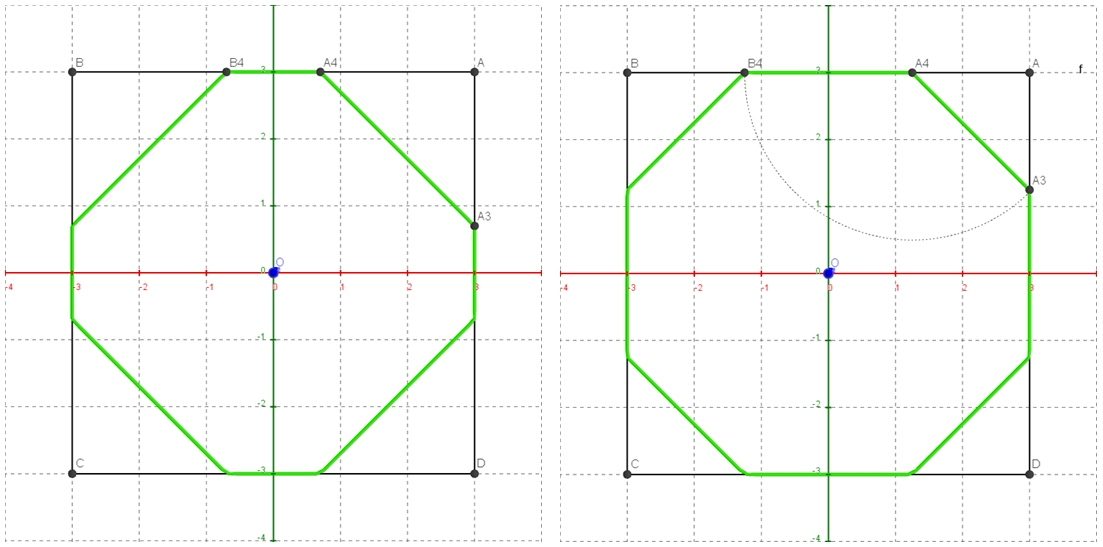
Or AA4 = k et A4B4 = 2a – 2k. Donc A3A4 = k √2, et on a l’équation : k √2 = 2a – 2k, d’où k = 2a /(2 + √2).
Ici k = 2x3 /(2 + √2) ≈ 1.7573 ≈ 1.75. Plus arc de cercle … !
3°) Si k augmente, les segments tels que A4B4 diminuent, et sont nuls si k = a !
Dans la discussion #3, on cherche à rendre l’objet rouge en rhombicuboctaèdre, donc avec ses faces carrées, le 8 autres en coins étant triangulaires équilatérales. On a le même problème que pour l’octogone !!! Donc e1 = a √2.
Et c’est pareil en discussion #4 ; Donc k = 2a /(2 + √2). Voici les 2 figures … avec a=b=c=3 !
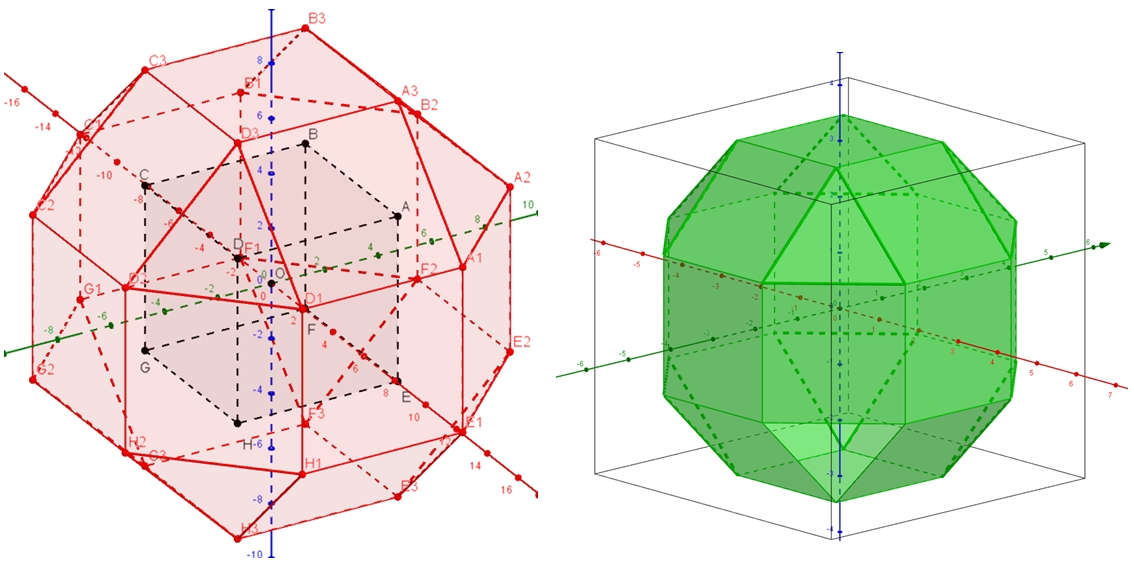
Voilà pour les corrigés.
La suite vous montre en 6 étapes le passage du cube à son octaèdre dual, en passant par le rhombicuboctaèdre pour k = 2.9 (environ).
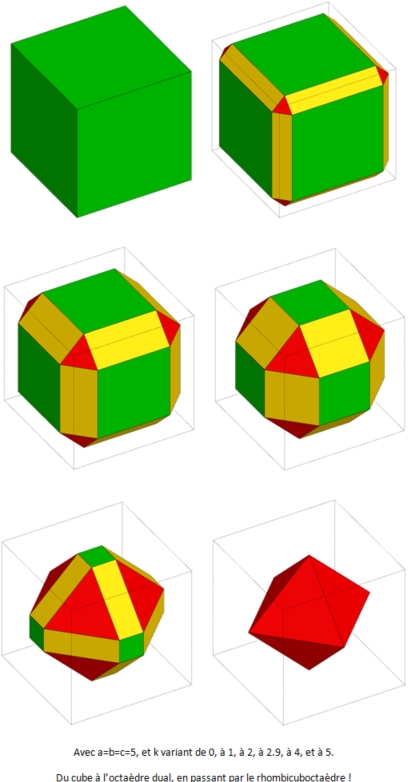
Et le lien pour le programme GeoGebra, si ça passe ... !
https://cjoint.com/c/KEht3aLzt3f
https://cjoint.com/doc/21_05/KEht3aLzt3 … -05-07.ggb
Bonne soirée, Bernard-maths
Dernière modification par Bernard-maths (14-06-2021 10:11:26)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#6 08-05-2021 09:46:26
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour Bernard-maths,
... Bonjour à Wiwaxia, qui m'a "obligé" à ouvrir cette discussion ... :-)))
Après avoir parlé des équations de polyèdres (Voir : "La réduction des polyèdres convexes à l'intersection de demi-espaces"), je vais vous parler de 2 applications sur ces polyèdres (et peut-être d'autres).
La première concerne les courbes (en 2D) et les surfaces (en 3D) des polygones ou polyèdres, qui consiste, pour imager, à les faire grossir en dehors de l'objet de départ.
La deuxième concerne les troncatures, consistant à "découper" l'objet selon quelques "consignes".
Les deux activités peuvent être mises en relation, dans certains cas (pas tous !), d'où la même discussion ...
Loin de moi l'intention de perturber tes projets d'exposés.
Tu construit des figures très claires, qui mettent bien en évidence la parenté et les élément de symétrie des objets représentés.
En ce qui concerne la troncature par un plan, il suffit d'introduire une face supplémentaire, d'orientation et de distance au centre arbitraires; le principe en a déjà été donné.
Voir le message #09 dans http://www.bibmath.net/forums/viewtopic.php?id=13806
Je n'ai pas répondu jusque là, car je me suis investi dans le traitement des images et dois par ailleurs assumer des obligations aussi lourdes que diverses.
Cordialement,
W.
Hors ligne
#7 08-05-2021 10:32:18
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour Wiwaxia !
bien sur je plaisantais ... :-)))
Je sais que tu es très occupé avec tes nouvelles attributions.
Je suis moi aussi bien pris, car il y aurait beaucoup à dire sur les équations que je développe ! Et je découvre encore divers aspects ...
Et je n'ai pas encore bien dit quelles étaient les équations possibles pour un rhombocubictaèdre !
Et les variantes sur les équations !!!
Mais c'est pour après, juste le prochain baratin ...
Alors, bon suivi ... cordialement, Bernard-maths
Dernière modification par Bernard-maths (08-05-2021 10:33:36)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#8 09-05-2021 16:51:44
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour à tous !
Remarque importante : à partir d’un parallélépipède rectangle, nous avons établi son équation de volume plein. Puis en ajoutant un paramètre, nous avons obtenu d’autres polyèdres enveloppes (surfaces de niveaux), avec leurs équations de surfaces. Enfin nous avons aussi pu obtenir des polyèdres de troncatures, et leurs équations de surfaces.
En jouant sur les valeurs des paramètres de dimension a, b et c du parallélépipède rectangle, on peut obtenir de multiples polyèdres, et aussi à partir d’un rectangle (si c = 0), ou d’un segment (si b = c = 0), ou même d’un point (a = b = c = 0).
Enfin, dans le cas a = b = c, nous avons des polyèdres générés autour du cube, et au passage des équations de rhombicuboctaèdres !
La méthode utilisée apporte donc une grande variété d’équations de polyèdres, mais que je n’ai trouvée utilisée nulle part, pour le moment, et à ma connaissance. Et de plus, elle semble utilisable sur tout polygone ou polyèdre convexe …
Voici ce que ça donne pour un cube ...
EQUATIONS des RHOMBICUBOCTAEDRES associés à un CUBE. Car il y en deux !
Soit un cube centré en l’origine d’un repère, et dont les sommets ont pour coordonnées (±a ; ±a ; ±a), a réel ≥ 0.
Alors une équation de ce cube, en tant que volume plein, est :
abs(x + a) + abs(x - a) + abs(y + a) + abs(y - a) + abs(z + a) + abs(z - a) = 6a.
Soit e un réel > 0, et soit l’équation :
abs(x + a) + abs(x - a) + abs(y + a) + abs(y - a) + abs(z + a) + abs(z - a) = 6a + 2e.
Cette équation correspond, pour chaque valeur de e, à un polyèdre extérieur au cube. Polyèdre constitué de 26 faces.
6 des faces sont des carrés isométriques des 6 faces du cube, et à la distance e du cube ; 12 faces sont des rectangles, joignant 2 à 2 les 6 faces carrées, en correspondance des 12 arêtes du cube ; enfin 8 faces sont des triangles équilatéraux, joignant les faces rectangulaires 3 par 3, en correspondance des 8 sommets du cube.
Dans le cas où e = a√2, alors le polyèdre est un rhombicuboctaèdre, dont l’équation est :
abs(x + a) + abs(x - a) + abs(y + a) + abs(y - a) + abs(z + a) + abs(z - a) = 2a(3 + √2).
Soit un réel k, 0 < k ≤ a. Et l’équation du cube plein, centré en l’origine, et d’arête 2(a – k), intérieur au 1er cube, et à la distance k :
abs(x + a-k) + abs(x – a+k) + abs(y + a-k) + abs(y – a+k) + abs(z + a-k) + abs(z – a+k) = 6(a – k).
Puis l’équation :
abs(x + a-k) + abs(x – a+k) + abs(y + a-k) + abs(y – a+k) + abs(z + a-k) + abs(z – a+k) = 6(a – k) + 2k.
Cette équation correspond, pour chaque valeur de k, à un polyèdre surface de niveau pour le 2ème cube, dont les faces carrées sont à la distance k du 2ème cube, et donc situées sur les faces carrées du 1er cube, "concentrique". Ce qui correspond à un polyèdre de troncature du 1er cube. Polyèdre constitué de 26 faces.
Dans le cas où k = a(2 - √2) , alors le polyèdre est un rhombicuboctaèdre, dont l’équation est :
abs(x + a-k) + abs(x – a+k) + abs(y + a-k) + abs(y – a+k) + abs(z + a-k) + abs(z – a+k) = 6a – 4 a(2 - √2), soit :
abs(x + a-k) + abs(x – a+k) + abs(y + a-k) + abs(y – a+k) + abs(z + a-k) + abs(z – a+k) = 2a(2√2 – 1).
Voici une vue des 2 rhombicuboctaèdres, obtenue avec le logiciel "maple" et paint (l'ancien !) :
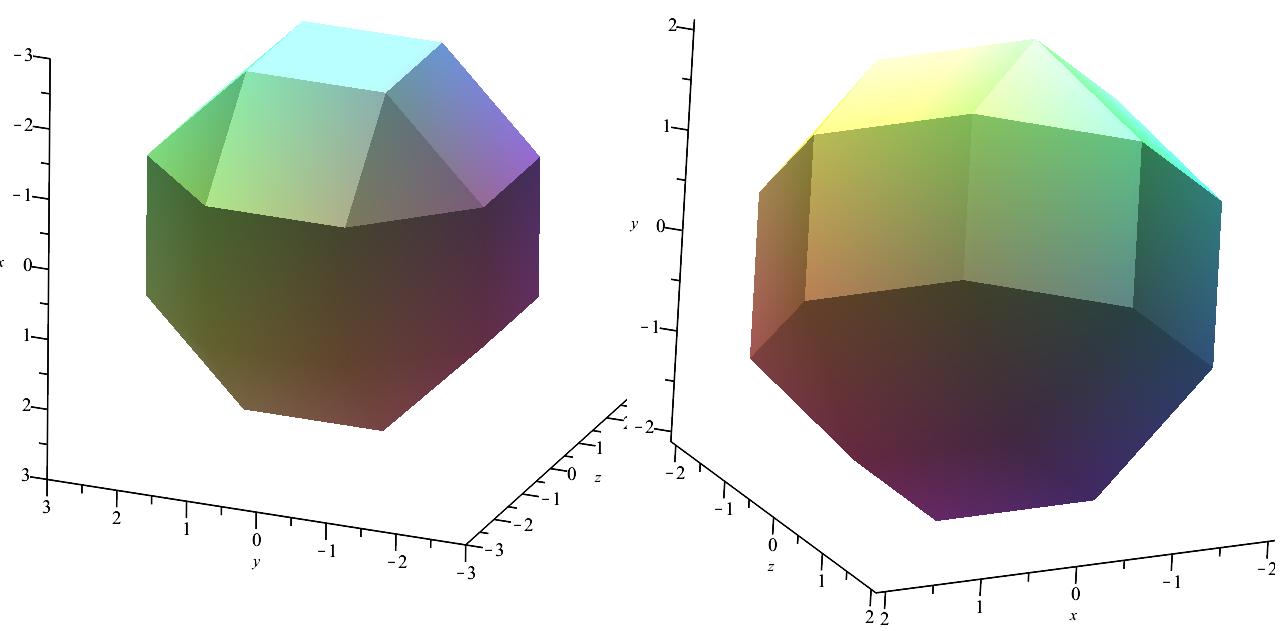
Avec a = 1, et vers l'extérieur, puis avec a = 2, et vers l'intérieur.
Cordialement, Bernard-maths
Dernière modification par Bernard-maths (24-09-2021 19:09:23)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#9 14-05-2021 15:38:54
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour à tous !
Je voudrais vous apporter quelques variations sur l'équation "bleue". En effet, si n réel > 0, alors on peut regrouper les 2 termes de chaque variable, et les élever à la puissance n, ainsi que le second membre :
[abs(x+a-k)+abs(x–a+k)]^n+[abs(y+a-k)+abs(y–a+k)]^n+[abs(z+a-k)+abs(z–a+k)]^n=[6(a–k)+2k]^n.
Ceci a pour effet de provoquer, au niveau des troncatures, un arrondi de ce qui était des rectangles et triangles équilatéraux.
Mais les faces carrées restent plates et carrées !
Je dois encore développer un peu cet aspect, avec quelques figures sur des cas particuliers de n. Lorsque n > 1, on a des arrondis "sortants", et si 0 < n < 1, les arrondis sont "rentrants". Je crois que pour s'inspirer de la forme des arrondis, on peut penser au "super-cube" d'équation : abs(x)^n + abs(y)^n + abs(z)^n = a^n ... à vérifier !
Eh bien alors, à plus !
Bernard-maths
Dernière modification par Bernard-maths (18-05-2021 09:41:22)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#10 25-05-2021 06:16:58
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour à tous !
J'ai eu pas mal d'occupations "annexes", mais j'ai pu cogiter un peu les maths ... et ce matin je ne vais pas vous donner des exemples de variations avec les exposants, ce sera pour plus tard ... En contrepartie, je vais vous parler rapidement de l'octaèdre, et de ses surfaces de niveaux, en troncature du cube, pour aboutir au cuboctaèdre !
On connaît une équation de l'octaèdre en tant que surface : abs(x) + abs(y) + abs(z) = b, où b est un réel positif, et les 6 sommets sont A(b,0,0), B(0,b,0), C(-b,0,0), D(0,-b,0), E(0,0,b) et F(0,0,-b). Il est le dual d'un cube PQRSTUVW, avec P(b,b,b), Q(-b,b,b), R(-b,-b,b), S(b,-b,b) pour la face "du haut", puis T(b,b,-b), U(-b,b,-b), V(-b,-b,-b) et W(b,-b,-b) "en bas". Quand on dit "dual", cela signifie ici que A, B, etc ... sont les centres des faces PSWT, etc ... du cube, voir figure !
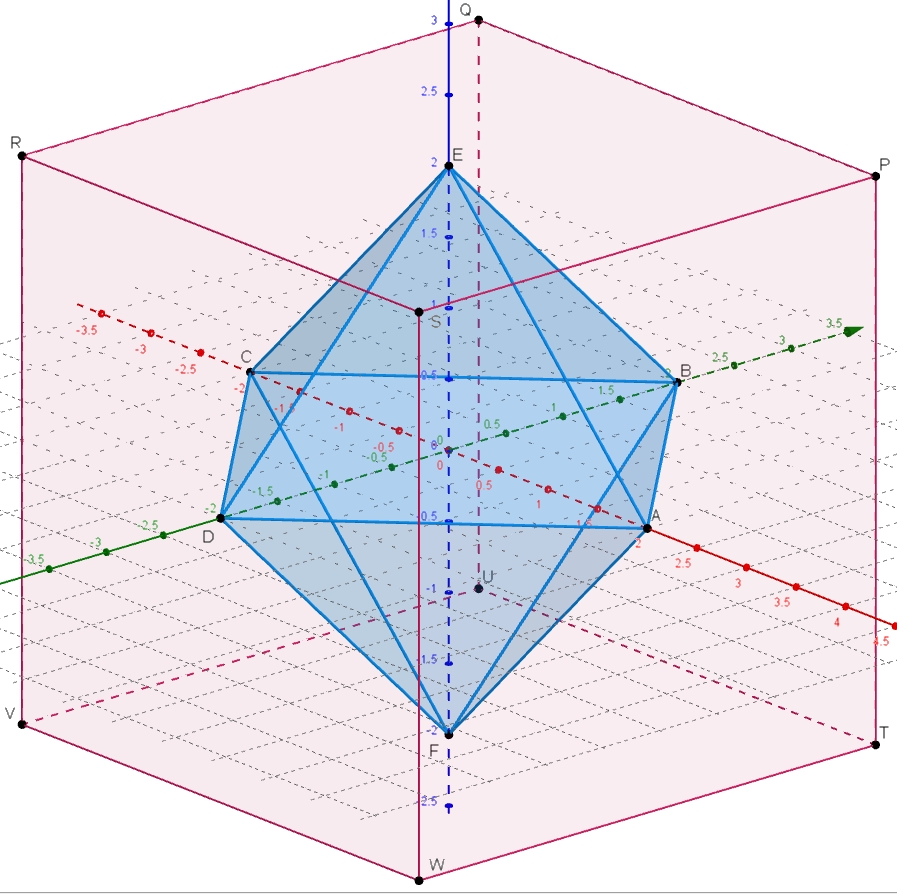
Partant de l'équation de surface de l'octaèdre, on en déduit des équations des 8 faces :
abs(-x - y - z + b), abs(x + y + z + b), abs(-x + y + z + b), abs(x - y - z + b), abs(x - y + z + b), abs(-x + y - z + b), abs(x + y - z + b), abs(-x - y + z + b) . La distance du centre O(0,0,0) à chaque face vaut b / √3 ... ce qui permet d'écrire une équation de l'octaèdre plein, donc du volume ! En multipliant par √3 ...
abs(-x - y - z + b) + abs(x + y + z + b) + abs(-x + y + z + b) + abs(x - y - z + b) + abs(x - y + z + b) + abs(-x + y - z + b) + abs(x + y - z + b) + abs(-x - y + z + b) = 8*b Ce qui donne ceci avec "maple" :
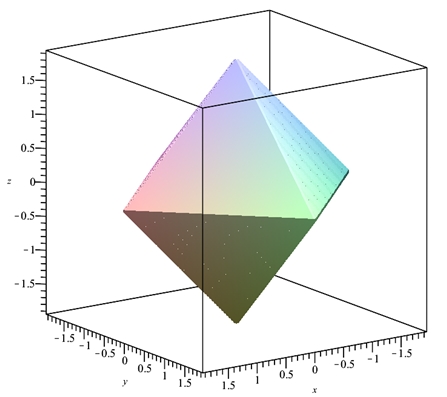
A partir de cette équation, on peut générer des équations de surfaces (de niveaux) extérieures en ajoutant une constante k positive à b, ou bien des équations de troncatures (de quoi ?) en retranchant la constante k à b ...
Dans un premier temps (j'y reviendrai un peu plus tard), nous allons voir ce qu'il se passe si on retranche k = b à b !
On obtient l'équation :
abs(-x - y - z) + abs(x + y + z) + abs(-x + y + z) + abs(x - y - z) + abs(x - y + z) + abs(-x + y - z) + abs(x + y - z) + abs(-x - y + z) = 8*b
Ce qui donne :
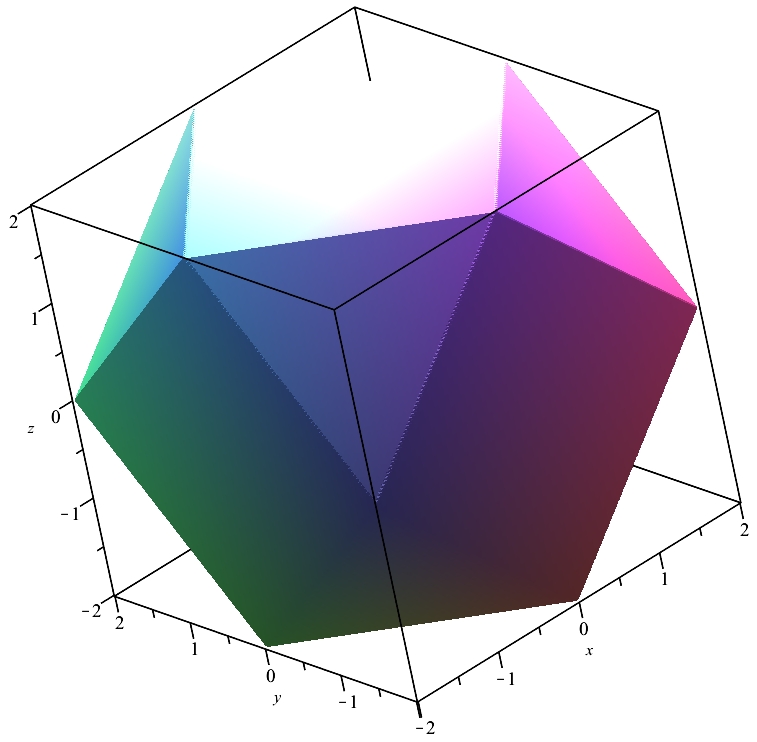
On reconnaît un cuboctaèdre ... En effet l'équation se simplifie, car les plans parallèles sont alors confondus :
abs(x + y + z) + abs(x - y - z) + abs(-x + y - z) + abs(-x - y + z) = 4*b
Equation publiée en 2007 par Rotaru Paul ! Et découlant ici naturellement de l'équation pleine de l'octèdre ...
Voilà pour le moment. Mais il reste quelques détails à préciser !... Il peut y avoir quelques os ?
Bernard-maths
Dernière modification par Bernard-maths (27-05-2021 06:25:55)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#11 27-05-2021 06:38:03
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour à tous !
Non, pas d'os ! Voyons la suite ...
Les 4 plans du cuboctaèdre sont « bien connus », ce sont les plans « hexagonaux » du cube, chacun passant par 6 milieux d’arêtes, et coupant le cube selon un hexagone régulier. Ce sont leurs équations qui donnent la « formule du cuboctaèdre ».
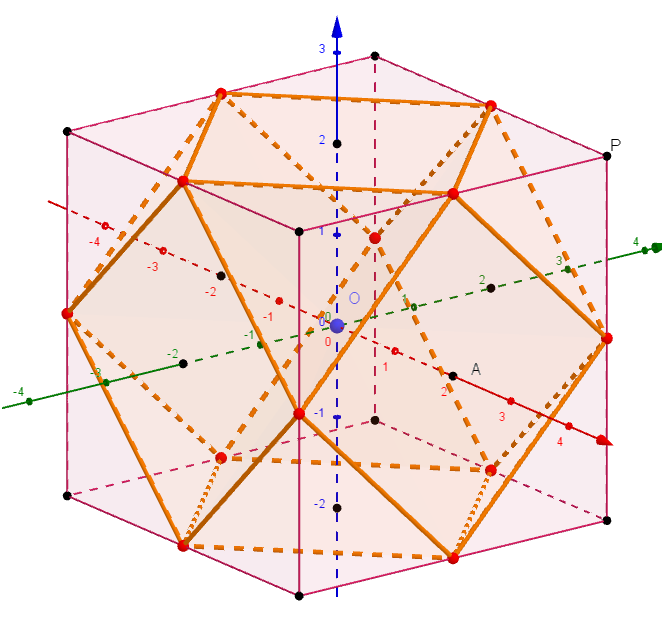
Sur cette figure, les milieux des arêtes du cube sont en rouge. On peut voir les 4 hexagones qui s'entrecroisent sur le cube.
Sur les faces du cube on a 6 carrés, et autour des sommets on a 8 triangles équilatéraux …
Le problème qu’on doit vérifier, est de savoir si l’équation du cuboctaèdre détermine les 6 carrés pleins, et les 8 triangles pleins. Vu les nombreuses symétries de la figure, et en particulier la symétrie centrale, de centre O, il suffit de montrer que le carré de centre A est défini en entier plein, et que le triangle face au sommet P est lui aussi défini en entier plein.
On peut considérer la figure suivante … dans laquelle on a construit les 6 pyramides de bases carrées, et laissé sans base les 8 pyramides englobant les sommets du cube, P … etc.
Sur la figure d’après on a affiché les 4 plans, et on peut se rendre compte (visuellement) que les pyramides carrées sont bordées par les 4 plans, alors que les pyramides triangulaires ne sont bordées que par 3 des 4 plans !
Nous allons chercher sur quels plans se trouvent les points situés dans la pyramide de base carrée de centre A, ainsi que les points situés dans la pyramide triangulaire contenant le point P.
Le point A n’est plus affiché, mais c’est celui d’abscisse 2 sur l’axe rouge des abscisses … P est au milieu de la figure.
Dans l'équation abs(x + y + z) + abs(x - y - z) + abs(-x + y - z) + abs(-x - y + z) = 4*b, nous allons remplacer chaque valeur absolue par son expression équivalente selon la pyramide dans laquelle on se place : "celle du point A", ou "celle du point P".
Pour cela, étudions le signe associé à chaque expression correspondant à chaque plan ...
Ainsi, pour le "1er plan" d'équation : x + y + z = 0, et pour tout point M(x,y,z) de l'espace, on associe la fonction f1(M) = x+y+z ... on sait que f(M) = 0 si, et seulement si, M appartient au "1er plan". Puis de chaque côté de ce plan, pour chaque demi-espace, on aura soit f1(M) > 0, soit f1(M) < 0 !
Le point A(b,0,0), avec b > 0. Calculons f1(A) = b + 0 + 0 = b > 0, donc abs(x+y+z) = x+y+z dans la pyramide contenant A ...
Calculons de même f2(A) = b - 0 - 0 = b > 0, donc abs(x-y-z) = x-y-z dans la pyramide contenant A, f3(A) = -b + 0 - 0 = -b < 0, donc abs(-x+y-z) = - (-x+y-z) = x-y+z dans la pyramide contenant A, enfin f4(A) = -b - 0 + 0 = -b < 0, donc abs(-x-y+z) = x+y-z ...
Finalement l'équation devient (dans la pyramide contenant A) : (x+y+z) + (x-y-z) + (x-y+z) + (x+y-z) = 4b, soit finalement x = b !
Donc dans la pyramide contenant A, l'équation se réduit à celle du plan d'équation x=b, ce qui le plan contenant la face du cube de centre A. Finalement on doit retenir de ce plan que la portion dans la pyramide, ce qui donne le carré plein de centre A, et de sommets les milieux des arêtes du cube !!!
=
Par symétries, ou par calculs similaires, on trouve que l'équation abs(x + y + z) + abs(x - y - z) + abs(-x + y - z) + abs(-x - y + z) = 4*b comprend les 6 carrés plein du cuboctaèdre.
En procédant de même avec le point P(b,b,b) : f1(P) = 3b >0, abs(x+y+z) = x+y+z ; f2(P) = -b <0, abs(x-y-z) = -x+y+z ; f3(P) = -b <0, abs(-x+y-z) = x-y+z ; f4(P) = -b <0, abs(-x-y+z) = x+y-z.
On trouve finalement pour équation "réduite" : 2x + 2y + 2z = 4b. équation d'un plan passant par les 3 milieux d'arêtes du cube, [PQ], [PS] et [PT], soit le triangle équilatéral plein !
Par symétries, ou par calculs similaires, on trouve que l'équation abs(x + y + z) + abs(x - y - z) + abs(-x + y - z) + abs(-x - y + z) = 4*b comprend les 8 triangles équilatéraux pleins du cuboctaèdre.
En conclusion, l'équation abs(x + y + z) + abs(x - y - z) + abs(-x + y - z) + abs(-x - y + z) = 4*b est celle du cuboctaèdre !
Dernière modification par Bernard-maths (27-05-2021 07:58:46)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#12 27-05-2021 18:43:06
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonsoir ! Un petit cinéma ... Du tétraèdre De l'octaèdre au cuboctaèdre en 9 figures !

Dernière modification par Bernard-maths (11-06-2021 08:41:17)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#13 08-06-2021 00:54:09
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonsoir Bernard-Maths,
Les figure sont bien faites mais un peu étranges, difficiles à situer dans le cube représenté en perspective.
Du tétraèdre au cuboctaèdre en 9 figures !
Le premier solide est un octaèdre , et non un tétraèdre.
Il faudrait épaissir les 3 arêtes antérieures du cube repère pour mieux appréhender le relief.
Hors ligne
#14 10-06-2021 22:13:07
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonsoir Wiwaxia !
Certes, mais quand on est généreux, on ne compte pas !
JE RECTIFIE ! Merci.
Oui, les choses évoluent, et je trouve de nouvelles équations ; il faudra que je me remette sur bibmath pour les présenter ...
Je suis très pris ces derniers temps, et toi, comment va ton boulot ?
Je ne comprends pas comment je suis connecté ! Je n'ai rien demandé ...
A bientôt, Bernard-math
Dernière modification par Bernard-maths (11-06-2021 08:42:19)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#15 11-06-2021 08:19:02
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 991
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour,
Je ne comprends pas comment je suis connecté ! Je n'ai rien demandé ...
Si je comprends bien ton interrogation, tu as ouvert ton navigateur et hop, te voilà connecté sur Bibmath en tant que Bernard-math ?
Si c'est bien cela, la dernière fois que tu t'es identifié dur Bibmath, tu as dû cocher la case : se souvenir de moi lors de ma prochaine visite.
De quel navigateur te sers-tu ?
As-tu mis en place une gestion personnalisée des cookies ?
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#16 11-06-2021 08:37:42
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour Yoshi !
Je me suis mis sur le site voyant que Wiwaxia avait fait un tour.
Pour répondre j'allais m'identifier lorsque j'ai constaté l'être déjà !?
D'où ma remarque, à toute fin utile ...
J'utilise gmail, et je ne gère pas les cookies ... et je préfère me connecter à chaque fois, jamais coché la case de souvenir !
Bonne journée :-)
Dernière modification par Bernard-maths (11-06-2021 08:43:36)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#17 14-06-2021 08:49:14
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour à tous !
Après le cub et l'octaèdre, passons au dodécaèdre !
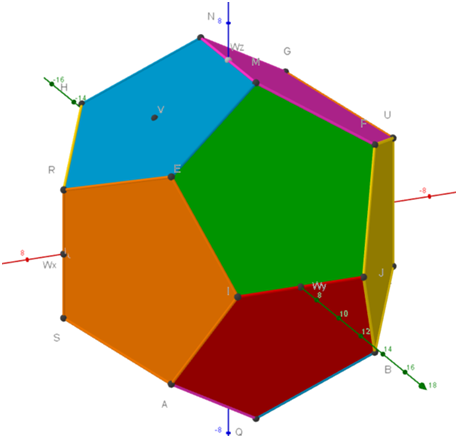
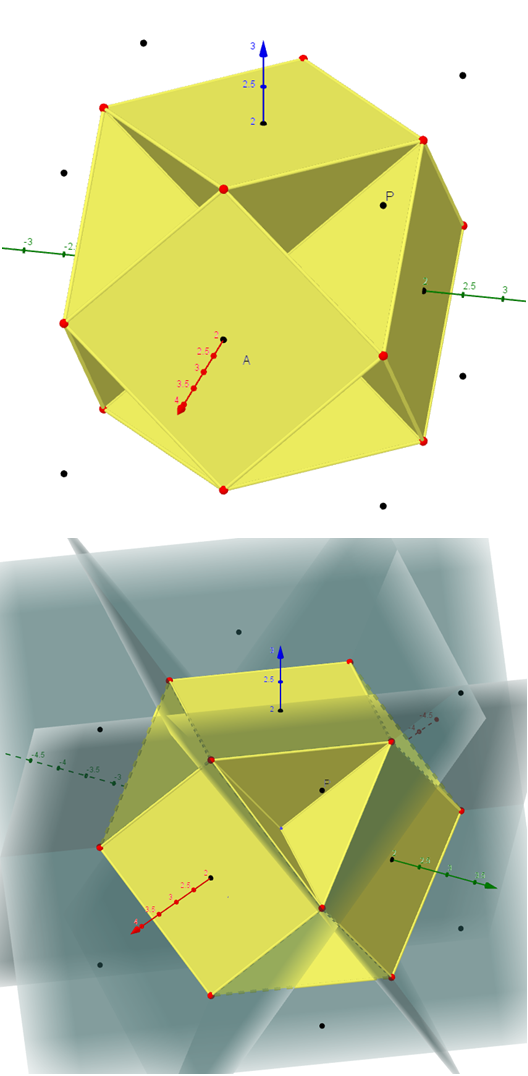
Figure avec GeoGebra, en 6 couleurs. V est l'isobarycentre de la face bleue (visible).
Celui-ci a été construit en prenant, sur le site de « mathcurve.com », les coordonnées des sommets, ce qui permet de faire des comparaisons pour la suite des manipulations !
Chaque sommet est commun à 3 faces, ce qui donne pour les 12 faces : 12 fois 5 divisé par 3 = 20 sommets …
Ce polyèdre possède des propriétés, à voir sur mathcurve …
Pour en trouver une équation cartésienne implicite, nous allons voir plusieurs méthodes !
Ces méthodes se réfèrent aux 12 plans des 12 faces, ou aux 6 plans parallèles aux faces, et passant par le centre du dodécaèdre. Nous allons en voir 2 !
Mais d’abord donnons les équations des 18 plans concernés … à lire sur les figures.
La 1ère image donne les plans verts (p_4 …) et jaunes (p_5 …).

La 2ème les plans bleus (q_4 …) et mauves (q_5 …).

Et la 3ème les plans oranges (r_4 …) et rouges (r_5 …).

Pour bien lire les formules, il faut considérer a/2 comme fraction, multipliée par phi^3 !
Ici phi est le "nombre d'or", et vaut : phi = (1+sqrt(5))/2 = 1.6183 ...
Je vais commencer par l’équation utilisant les 6 plans. Cette équation est écrite avec le logiciel « maple ».
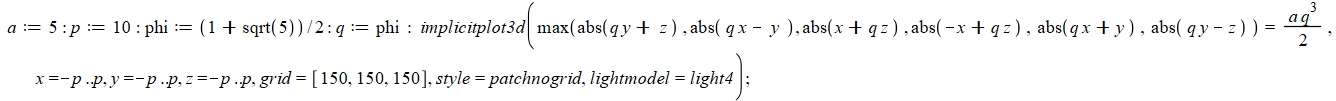
qui produit la figure suivante, d’un dodécaèdre « surface » :
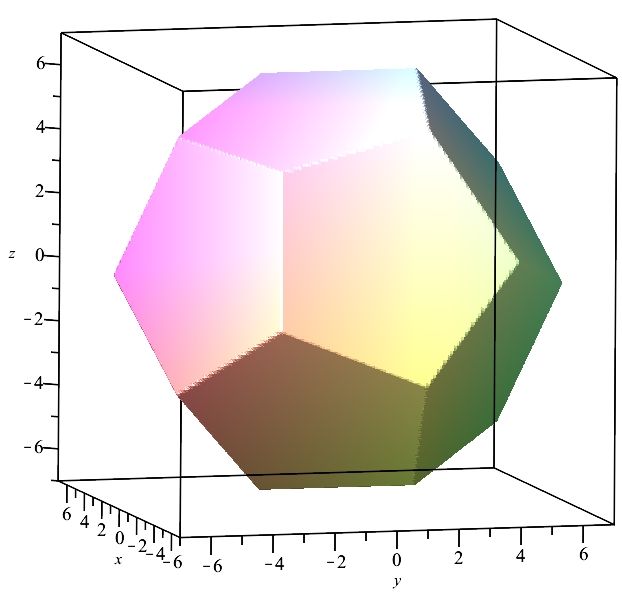
Pour le moment, je n’ai pas d’extension de figure en vue avec cette équation. En effet, si on ajoute une constante au membre de droite, on obtient un dodécaèdre plus grand ou plus petit, selon le signe de la constante …
La valeur a q^3 / 2 est celle qui donne le dodécaèdre avec les sommets donnés au début !
Passons maintenant à la deuxième forme d’équation. Il s’agit d’en définir une équation « pleine ».
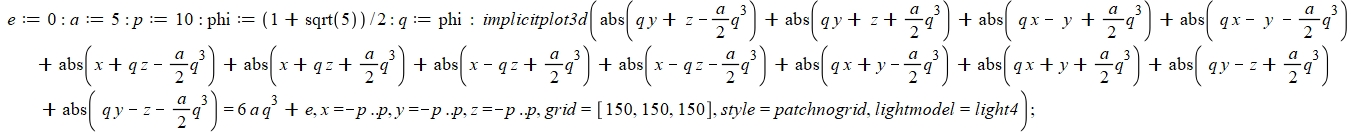
Elle est aussi écrite sur « maple » et donne les résultats suivant :
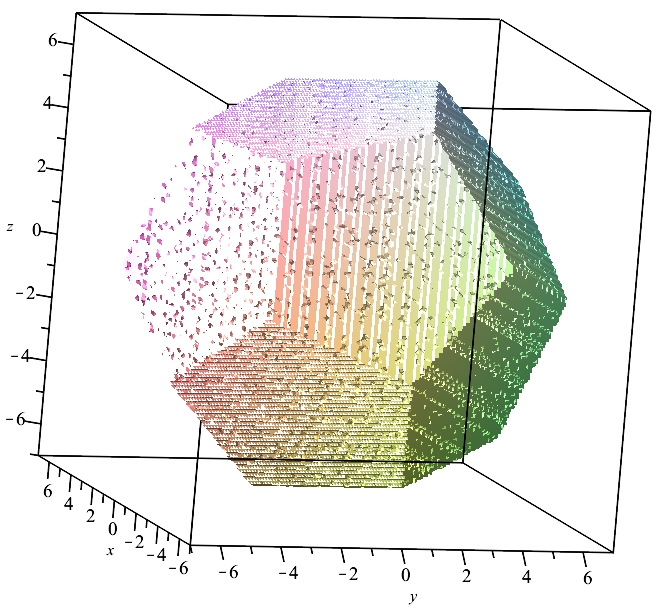
Les 2 figures sont sous les mêmes angles … mais on voit que la 2ème est pleine d’irrégularités. Il s’agit d’une équation de polyèdre plein, et les logiciels sont « piégés » par leur algorithme … qui « s’attend plutôt à des surfaces » ??? (C'est moi qui le dit ...)
MAIS c’est beau quand même ! Et on peut « déformer la figure », en « déformant l’équation » … par une constante par exemple ! Mais on pourrait essayer autre chose … avis aux curieux, il y a tant à essayer !!!
Maintenant, je vais ajouter une constante. Il faut « se rappeler » qu’une telle équation « pleine » correspond à un membre de gauche MINIMAL (somme de distances la plus basse possible). Si on ajoute une constante positive au membre de droite, on va sortir de la contrainte « minimale », et engendrer une surface (de niveau) entourant le polyèdre obtenu.
Ici cette constante est représente par la variable e, qui vaut 0 pour le dodécaèdre plein. Je vais vous présenter un petit film des figures obtenues lorsque e varie de 0 à 20 000, et plus vers l’infini !
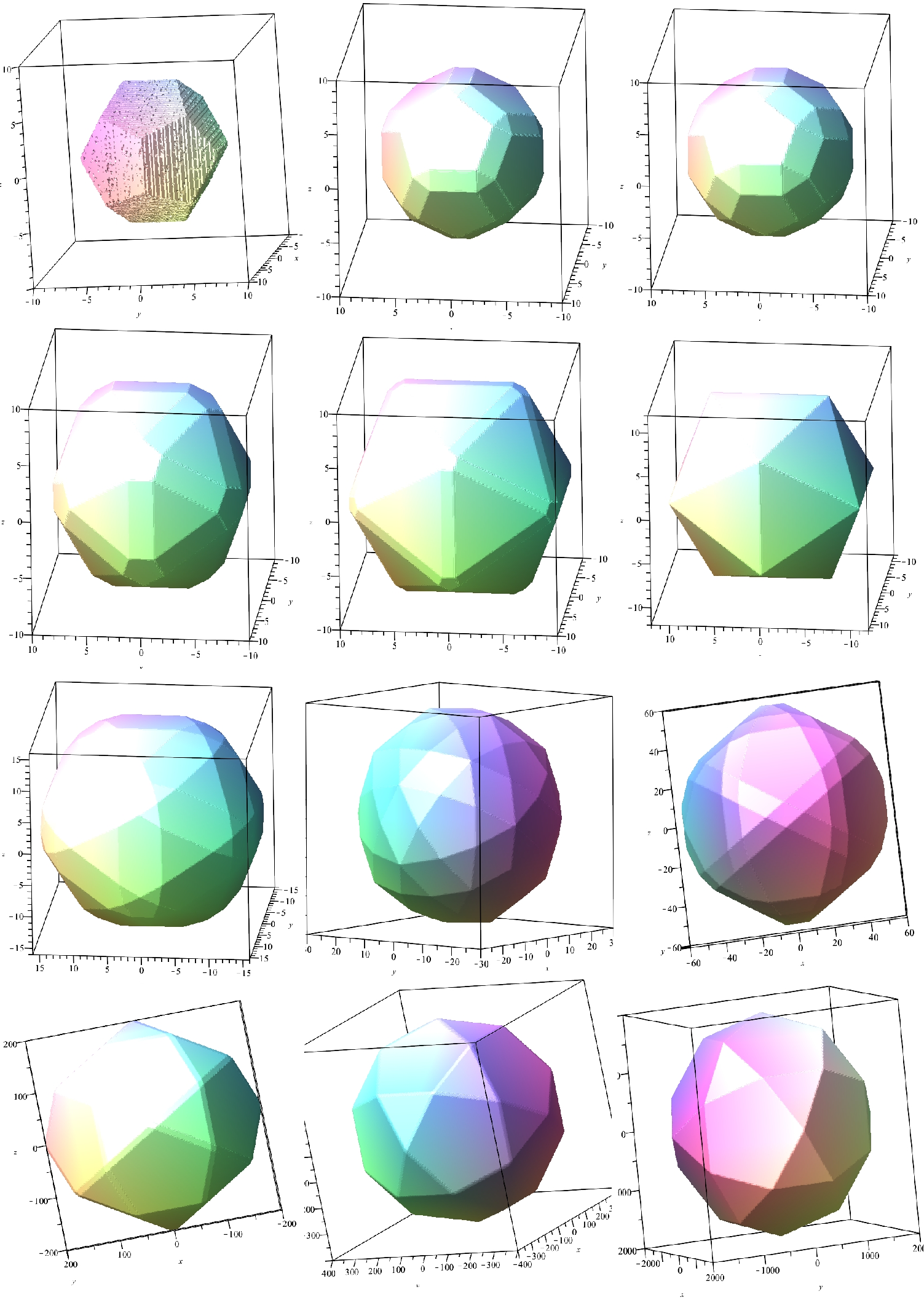
Les différentes valeurs de e sont dans l’ordre des 12 figures : 0, 4, 6, 12, 20, 26, 80, 200, 500, 800, 4 000,
et 20 000.
Ces valeurs ne sont pas forcément des valeurs exactes pour les phénomènes observés, mais sont indicatives …
En cours d’essai, les figures ont tourné et changé de format, car grandissantes … d'où les variations de présentation.
Pour les 6 premières figures, partant du dodécaèdre plein, on voit les faces pentagonales se réduire, les arêtes se déformer en rectangles, et surtout les sommets se transformer en triangles équilatéraux ! Résultat ? Un icosaèdre, figure de 20 triangles équilatéraux , figure duale d'un dodécaèdre !
MAIS ici, ce n’est pas le dual externe du dodécaèdre de départ. L’icosaèdre apparaît naturellement comme surface de niveau pour une valeur (précise à calculer !) du second membre.
Après ? Le nombre e augmentant, l’icosaèdre se déforme à son tour (fig 7, 8 et 9), puis on voit la formation de triangles équilatéraux et de pentagones, pour aboutir (à quel moment exactement ?) à un icosidodécaèdre !
ALORS ? Est-ce une tendance, une convergence, pour e tendant vers + l’infini ? Je n’ai pas fait de calculs, je constate ici visuellement !
Eh bien, expérience faite le 08-12-2021, avec e allant jusqu'à 10 000 000, et p à 1 000 000, on trouve le même icosidodécaèdre !!! On peut penser que ça reste vrai pour e tendant vers +infini ...
Car c’est très beau à voir … (autosatisfaction oblige ...)
Dernière modification par Bernard-maths (08-12-2021 21:31:43)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#18 14-06-2021 19:35:43
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Courbes et surfaces de niveaux ... et troncatures.
Car c’est très beau à voir … (autosatisfaction oblige ...)
Ce sont effectivement de belles figures, dont tu pourrais améliorer l'apparence en travaillant la palette de couleurs, et en cherchant à exprimer les "intensités" (r, v, b) par des fonctions appropriées dépendant des composantes de la normale à la face considérée (je ne connais pas les instructions disponibles sur Geogebra).
Les belles teintes s'obtiennent pour Max(r, v, b) ~ 255 - éviter si possible le blanc, identique à la couleur du fond ... Des essais rapides sont possibles en utilisant MsPaint.
C'est du bon travail.
PS: Je remarque que la teinte d'une face n'est pas uniforme: il y a donc une source virtuelle d'éclairage de l'objet à distance finie; pourquoi ne pas faire intervenir un éclairage coloré, ou plusieurs sources de lumière ?
Que donnerait un fond noir, et un repère (le cube) tracé en blanc ?
Dernière modification par Wiwaxia (14-06-2021 19:43:23)
Hors ligne
#19 14-06-2021 21:31:25
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonsoir Wiwaxia !
Je ne maitrise pas du tout encore les "coloriages" ! Je suis nouveau sur "maple", et je n'ai pas du tout eu le temps de m'occuper des couleurs ...
Geogebra permet de colorer les objets "identifiés", mais si je trace un objet, sa couleur est unique ! Si je le découpe en morceaux identifiables, je peux adapter les couleurs.
Avec maple, j'ai copié quelques "programmes", et je mets la figure que je veux, mais son coloriage ne m'est pas accessible ... pour le moment ?
C'est vrai qu'avec Paint, on peut jouer sur les couleurs, mais ça prend du temps, et ... je suis "pressé" eh eh !
Merci de suivre, et de tes conseils,
bonne soirée, bernard-maths
Dernière modification par Bernard-maths (14-06-2021 21:32:49)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#20 16-06-2021 12:39:24
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour Bernard-maths,
J'ai regardé ce que propose Maple: la coloration locale est bien envisagée soit en fonction de la position du point, soit en fonction de l'orientation de la normale (le vecteur gradient); il n'y est pas fait référence explicite au procédé de tracé du rayon lumineux - cela relève en fait du second procédé, et m'a peut-être échappé.
Cordialement,
W.
Si ces liens peuvent t'être utiles:
https://www.maplesoft.com/support/help/ … ath=plot3d
https://www.maplesoft.com/support/help/ … ot%2fcolor
https://www.maplesoft.com/support/help/ … fcolorfunc
https://www.maplesoft.com/support/help/ … olorscheme
https://www.maplesoft.com/support/help/ … Dquickview
https://www.maplesoft.com/support/help/ … yhedraplot
https://www.maplesoft.com/support/help/ … ath=geom3d
https://www.maplesoft.com/support/help/ … 2fpolyhedr
Hors ligne
#21 16-06-2021 20:46:59
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonsoir Wiwaxia !
Merci pour ces références, je les regarderai dès un moment "libre" ...
pour l'instant, c'est un peu "la course" aux équations ... peu importe la couleur !!!?
Bonne soirée, Bernard-maths
PS : je cherche le "triacontaèdre rhombique", dual de l'icosidodécaèdre ... pour le moment.
Dernière modification par Bernard-maths (16-06-2021 20:48:44)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#22 09-12-2021 22:09:53
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonsoir à tous, et à Wiwaxia !
Aujourd'hui j'ai trouvé une équation du triacontaèdre, je m'y suis mis il y a 2 jours, aux temps libres ...
Cet objet est présenté ici, car il n'apparaît pas dans la suite des 12 figures de la discussion #17. Alors que j'espérais le trouver, non ! Par contre, comme d'après Mathcurve, il est le dual de l'icocosidodécaèdre, je l'ai donc rajouté !
Pour les aspects techniques, j'en reparlerai en présentant les solides de Platon évoluant vers une forme rhombique, par "pyramidation" des faces ...

Equation sur Mapple :
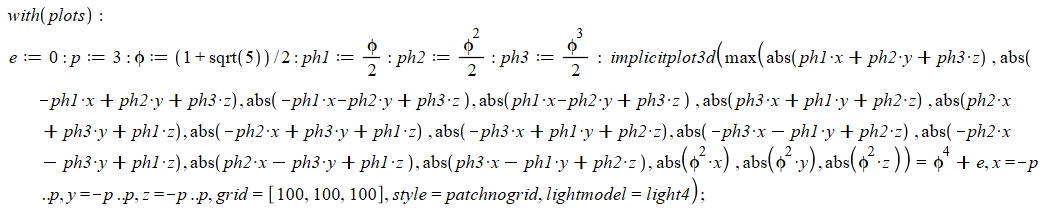
Voilà, bonne nuit, Bernard-maths
Dernière modification par Bernard-maths (10-12-2021 18:35:44)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#23 10-12-2021 09:12:05
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonjour Bernard-maths,
Pas mal, le résultat !
Je suppose que tu es parti de la liste des normales aux faces, qui passent par les milieux des arêtes du dodécaèdre ? Cela a dû être assez laborieux ...
Hors ligne
#24 10-12-2021 18:54:26
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Courbes et surfaces de niveaux ... et troncatures.
Bonsoir à tous !
Je vais vous présenter quelques exemples du "2ème principe" de courbe ou surface de niveau :
Exemple 1 : soit la courbe d'équation abs(x)n + abs(y)n = rn, et
la courbe associée abs[ abs(x)n + abs(y)n - rn = en ]. r le "rayon", n l'exposant et e "l'écart" ... > 0 ou =0.
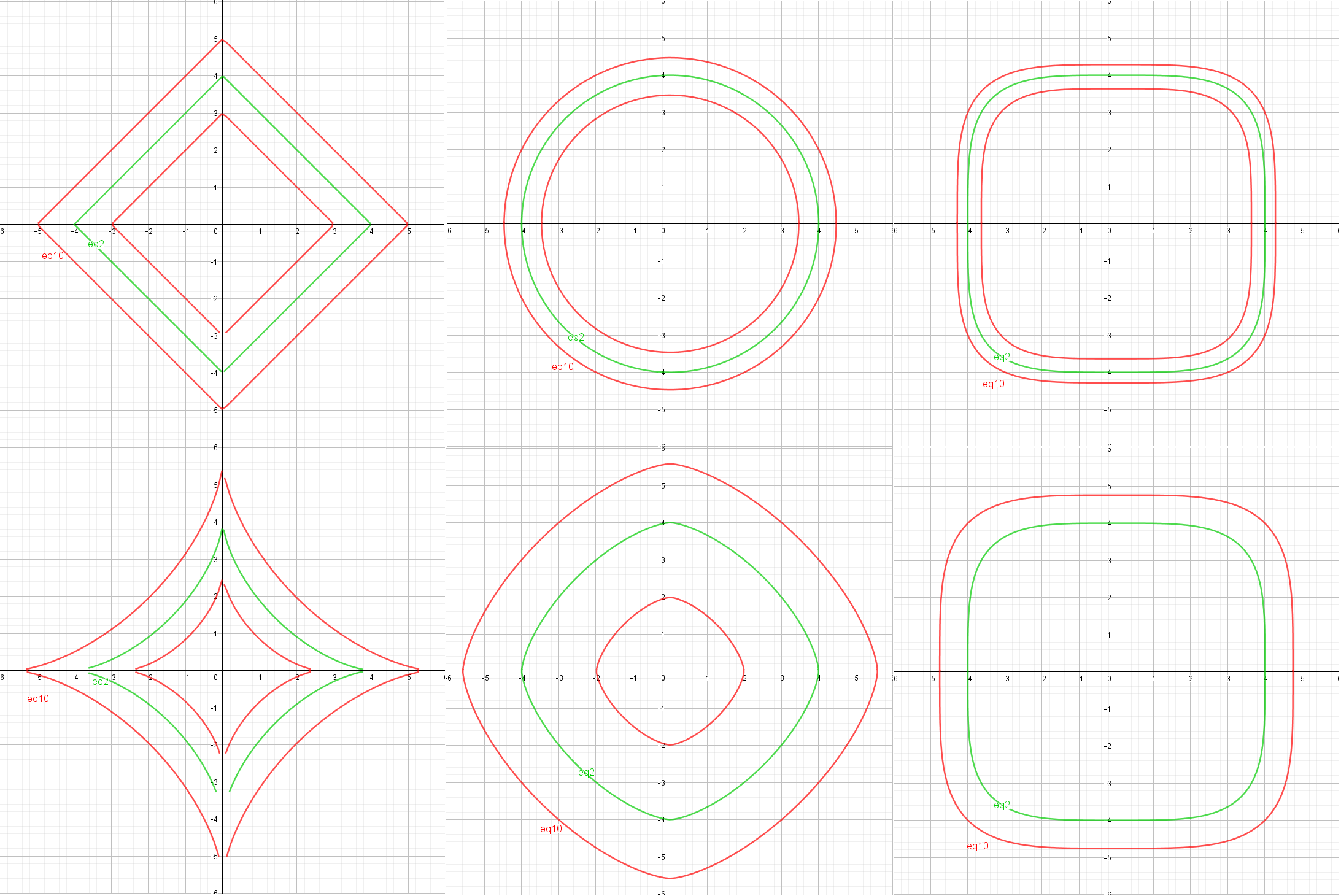
Pour les valeurs suivantes de n et e : 1 et 1 ; 2 et 2 ; 3 et 3 ; 2/3 et 1.5 ; 1.5 et 3 4 et 4 .
Notez que la courbe rouge est double ... SAUF si e est "trop grand", auquel cas la partie rouge intérieure disparaît !
Selon les valeurs de n, il faut ajuster e pour avoir ce qu'on veut .. je n'ai pas fait de calculs pour prévoir !!!
On peut même dupliquer le procédé (autant qu'on veut/peut ?),
par exemple : abs{abs[(abs(x))^n + (abs(y))^n - r^n] - e^n} = e'
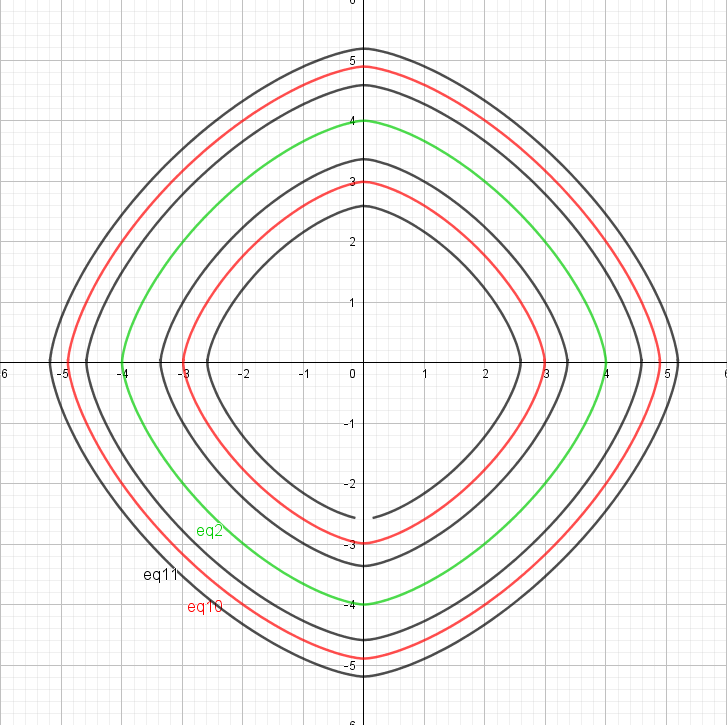
On voit se développer eq11 en double/double, autour des 2 parties de eq10 ... avec n = 1.5, e = 2, e' = 1.
N'hésitez pas à commenter, surtout si vous avez vu ça quelque part, ou du même genre, dites-le moi, merci !!!
La suite plus tard ... et Wiwaxia va en voir de belles !!! Bonne nuit.
Bernard-maths
Dernière modification par Bernard-maths (10-12-2021 21:59:02)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne








