Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#76 31-01-2021 15:00:12
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Bonjour à tous !
Je pense que tu cherches un moyen de projeter sur un plan une figure 3D ...
J'ai rencontré ce problème quand GeoGebra n'était pas encore en 3D, en 2003 pour mes terminales S.
J'ai supposé qu'on projetait la figure sur le plan (yOz), me semble-t-il, et j'utilisais des formules, à retrouver !
Donc la figure pouvait pivoter, et on affichait sa projection. J'ai utilisé ça avec GeoGebra 2D, et même (en 2003), avec Excel dans son module grapheur 3D ! Je pouvais même profiter de la gestion d'un curseur pour animer la figure.
Désolé, il faut que je retrouve les équations ... et ces lointaines figures !
Cordialement, Bernardmaths
Dernière modification par Bernard-maths (31-01-2021 15:02:20)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#77 06-02-2021 14:13:54
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Des équations et des cubes
Bonjour,
Je suis parvenu à mettre sur pied l'algorithme mettant en œuvre les notions précédentes, après une période chargée.
Je remercie Bernard-maths pour l'initiation de cette discussion, et les idées originales qu'il y a développées, qui m'ont permis d'envisager une nouvelle représentation des surfaces polyédriques
J'ai commencé très modestement par un cube, parce qu'il fallait boucler un programme assez lourd, et le purger de tous les bogues présents.

Le rhombicuboctaèdre présente un intérêt particulier en raison de la présence de 3 sortes de faces d'orientations remarquables; elles sont en effet normales
- soit aux axes du repère (axes quaternaires),
- soit à ses bissectrices (axes binaires),
- soit enfin aux axes ternaires (dans le cas des faces triangulaires).

https://fr.wikipedia.org/wiki/Petit_rho … a%C3%A8dre
https://mathcurve.com/polyedres/rhombic … edre.shtml
Les deux objets sont vus sous des perspectives voisines:
latitude (λ) = 10° , longitude (φ) = 20° puis 25° .
Il faut reprendre la définition des couleurs, ici arbitrairement reliées à l'orientation des normales aux faces dans le repère mobile (C, u1, u2, u3).
Dernière modification par Wiwaxia (06-02-2021 14:27:38)
Hors ligne
#78 06-02-2021 22:56:55
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Hello !
Ca rend bien, mais je vois que c'est lourd en programmation !
Perso, je viens de rééditer le cube tronqué, que j'avais dessiné il y a bien longtemps, GeoGebra 3D n'était pas là ...
Mais je n'ai pensé aux équations qu'il y a 3 ans, et en mars, pour les journées de Maths en scène, je vais le proposer en animation, ou en démonstration pour des terminales S ou post-bac ...
L'équation part du cube plein, et va vers l'octaèdre dual, équation valable pour toutes les figures intermédiaires.
Je vais tacher de le mettre en ligne cette semaine.
J'ai aussi commencé avec le tétraèdre et l'octaèdre, en choisissant bien leurs positions pour faciliter les démonstrations.
Bonne suite, Bernard-maths.
Dernière modification par Bernard-maths (06-02-2021 22:59:40)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#79 07-02-2021 07:09:22
- Daniel sevenou mahutondji
- Membre
- Inscription : 07-02-2021
- Messages : 1
Re : Des équations et des cubes
Bonjour,svp pour faire la dérivée partielle d'une fonction a plus de deux variables je sur posse que j'ai trois variables x,y,z où dans un premier instant je dérive x par rapport aux autres ,s'il était au carré que puis je faire pour eux merci
Hors ligne
#80 07-02-2021 09:29:10
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 988
Re : Des équations et des cubes
Bonjour Daniel,
N'as-tu pas vu que le nom de ce sous-forum était Le Coin des beaux problèmes de Géométrie ?
N'as-tu pas vu ce lien : Nouvelle discussion sur lequel tu aurais dû cliquer pour ouvrir TA propre discussion, choisir un titre clair et précis et y copier ta question.
Problème de vue ? Solution : consulter un ophtalmologue.
En effet, en quoi ta question, est-elle une réponse au sujet en cours ?
En rien, aucun rapport !...
Alors ?
Méconnaissance du sens du verbe Répondre ? Solution : consulter un dictionnaire.
Même si tu parasites ce sujet, je ne peux pas le fermer et gêner Wiwaxia et Bernard-maths, mais je veillerai à ce que tu n'aies pas de réponse...
Ne perds pas de temps, demain, je supprimerai ton message et le mien.*
Un dernier point.
Je t'invite à réfléchir à ce passage de nos Règles :
* Notre but étant de vous aider à résoudre vos difficultés, et non de faire les exercices à votre place, ne postez pas le sujet d'un exercice sans montrer que vous y avez travaillé : il n'y serait probablement pas répondu. A vous d'expliquer ce que vous avez déjà fait, là où vous bloquez, et pourquoi...
T'aider oui, faire le boulot à ta place, non.
Merci de ta compréhension.
Yoshi
- Modérateur -
Arx Tarpeia Capitoli proxima...
Hors ligne
#81 11-02-2021 15:43:29
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Des équations et des cubes
Bonjour,
Voici le programme source réalisant la mise en perspective du polyèdre à 26 faces:
PROGRAM Polyedre;
(*HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH
Représentation en perpective des faces d'un polyèdre
HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH*)
USES Crt, E_Texte, U_Copie_1F, Math, U_Math;
CONST N_Face = 26; Nf2 = N_Face DIV 2; // Nf2 = 13
TYPE Ve3D = RECORD x, y, z: Reel END;
Fxyz = FUNCTION(h, x, y, z: Reel): Reel;
Tab_Fxyz = ARRAY[1..N_Face] OF Fxyz;
Tab_Nf = ARRAY[1..Nf2] OF Ve3D;
Tab_Px = ARRAY[1..Nf2] OF Pixel;
VAR Vun1, Vun2, Vun3: Ve3D;
LstF: Tab_Fxyz;
LstN: Tab_Nf;
LstC: Tab_Px;
(*HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH
Equations des faces de polyèdre
HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH*)
FUNCTION F13(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
r:= h - z; s:= x + y; p:= Abs(r + s);
r:= h + z; q:= Abs(r - s);
r:= p + q; s:= 2 * h;
Result:= r - s
END;
FUNCTION F12(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
r:= h - y; s:= z + x; p:= Abs(r + s);
r:= h + y; q:= Abs(r - s);
r:= p + q; s:= 2 * h;
Result:= r - s
END;
FUNCTION F11(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
r:= h - x; s:= y + z; p:= Abs(r + s);
r:= h + x; q:= Abs(r - s);
r:= p + q; s:= 2 * h;
Result:= r - s
END;
FUNCTION F10(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
r:= h - x; s:= y + z; p:= Abs(r - s);
r:= h + x; q:= Abs(r + s);
r:= p + q; s:= 2 * h;
Result:= r - s
END;
FUNCTION F9(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
s:= z - x; p:= Abs(h - s); q:= Abs(h + s);
r:= p + q; s:= 2 * h; Result:= r - s
END;
FUNCTION F8(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
s:= z + x; p:= Abs(h - s); q:= Abs(h + s);
r:= p + q; s:= 2 * h; Result:= r - s
END;
FUNCTION F7(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
s:= y - z; p:= Abs(h - s); q:= Abs(h + s);
r:= p + q; s:= 2 * h; Result:= r - s
END;
FUNCTION F6(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
s:= y + z; p:= Abs(h - s); q:= Abs(h + s);
r:= p + q; s:= 2 * h; Result:= r - s
END;
FUNCTION F5(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
s:= x - y; p:= Abs(h - s); q:= Abs(h + s);
r:= p + q; s:= 2 * h; Result:= r - s
END;
FUNCTION F4(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
s:= x + y; p:= Abs(h - s); q:= Abs(h + s);
r:= p + q; s:= 2 * h; Result:= r - s
END;
FUNCTION F3(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
p:= Abs(h - z); q:= Abs(h + z);
r:= p + q; s:= 2 * h;
Result:= r - s
END;
FUNCTION F2(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
p:= Abs(h - y); q:= Abs(h + y);
r:= p + q; s:= 2 * h;
Result:= r - s
END;
FUNCTION F1(h, x, y, z: Reel): Reel;
VAR p, q, r, s: Reel;
BEGIN
p:= Abs(h - x); q:= Abs(h + x);
r:= p + q; s:= 2 * h;
Result:= r - s
END;
PROCEDURE InitF(VAR L_F: Tab_Fxyz);
BEGIN
L_F[ 1]:= F1; L_F[ 2]:= F2; L_F[ 3]:= F3;
L_F[ 4]:= F4; L_F[ 5]:= F5; L_F[ 6]:= F6;
L_F[ 7]:= F7; L_F[ 8]:= F8; L_F[ 9]:= F9;
L_F[10]:= F10; L_F[11]:= F11; L_F[12]:= F12; L_F[13]:= F13;
END;
(*HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH
Initialisation des fonctions
HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH*)
FUNCTION CombLin3V(C1, C2, C3: Z_32; V1, V2, V3: Ve3D): Ve3D;
VAR W: Ve3D;
BEGIN
WITH W DO
BEGIN
x:= C1 * V1.x; IncR(x, C2 * V2.x); IncR(x, C3 * V3.x);
y:= C1 * V1.y; IncR(y, C2 * V2.y); IncR(y, C3 * V3.y);
z:= C1 * V1.z; IncR(z, C2 * V2.z); IncR(z, C3 * V3.z)
END;
Result:= W
END;
FUNCTION F_Face(A1, B1, X1, Y1, Z1: Z_32): Byte;
CONST Seuil = 1E-10;
VAR j, Jf: Byte; A2, A3: Z_32; r: Reel; W: Ve3D;
BEGIN
W:= CombLin3V(X1, Y1, Z1 + 1, Vun1, Vun2, Vun3);
Jf:= 0; A2:= A1 + B1; A3:= A2 + B1;
FOR j:= 1 TO 3 DO BEGIN
r:= LstF[j](A1, W.x, W.y, W.z);
IF (r>Seuil) THEN Jf:= j
END;
FOR j:= 4 TO 9 DO BEGIN
r:= LstF[j](A2, W.x, W.y, W.z);
IF (r>Seuil) THEN Jf:= j
END;
FOR j:= 10 TO Nf2 DO BEGIN
r:= LstF[j](A3, W.x, W.y, W.z);
IF (r>Seuil) THEN Jf:= j
END;
Result:= Jf
END;
FUNCTION F_Polyedre(A1, B1, X1, Y1, Z1: Z_32): Reel;
VAR j: Byte; A2, A3: Z_32; s: Reel; W: Ve3D;
BEGIN
W:= CombLin3V(X1, Y1, Z1, Vun1, Vun2, Vun3);
s:= 0; A2:= A1 + B1; A3:= A2 + B1;
FOR j:= 1 TO 3 DO IncR(s, LstF[j](A1, W.x, W.y, W.z));
FOR j:= 4 TO 9 DO IncR(s, LstF[j](A2, W.x, W.y, W.z));
FOR j:= 10 TO Nf2 DO IncR(s, LstF[j](A3, W.x, W.y, W.z));
Result:= s
END;
PROCEDURE Calc_Mat_Im2(La, Ha: Z_32; VAR Ma2: Tab_Pix);
CONST Seuil = 1E-10; P000: Pixel = (0, 0, 0);
VAR Icoul: Byte;
Apol,Bpol, Rcen, Xcen, Ximg, Xm, Ycen, Yimg, Ym, Zimg, Zmin: Z_32;
u: Reel; Px: Pixel;
BEGIN
Xcen:= La DIV 2; Ycen:= Ha DIV 2;
IF (La<Ha) THEN Rcen:= Xcen
ELSE Rcen:= Ycen;
Zmin:= -2 * Rcen;
Apol:= Round(0.8628 * Rcen); Bpol:= Round(0.3574 * Rcen);
FOR Xm:= 0 TO (La - 1) DO
BEGIN
Ximg:= Xm - Xcen;
FOR Ym:= 0 TO (Ha - 1) DO
BEGIN
Yimg:= Ym - Ycen; Zimg:= 0; We(10, 40, Xm, 6);
REPEAT
Dec(Zimg);
u:= F_Polyedre(Apol, Bpol, Ximg, Yimg, Zimg + Rcen)
UNTIL ((u<Seuil) OR (Zimg=Zmin));
IF (Zimg=Zmin) THEN Px:= P000
ELSE BEGIN
Icoul:= F_Face(Apol, Bpol, Ximg, Yimg,
Zimg + Rcen);
Px:= LstC[Icoul]
END;
Ma2[Xm,Ym]:= Px
END
END
END;
(*HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH
Détermination de la couleur des faces en fonction de leur orientation
HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH*)
FUNCTION Pscal(W1, W2: Ve3D): Reel;
VAR p: Reel;
BEGIN
p:= W1.x * W2.x; IncR(p, W1.y * W2.y);
IncR(p, W1.z * W2.z); Result:= p
END;
PROCEDURE InitC(VAR L_C: Tab_Px);
CONST M1 = 240; M2 = 255.449;
VAR j, k: Byte; m, p, q, r, s, u, v, w: Reel; Px: Pixel;
BEGIN
FOR j:= 1 TO Nf2 DO
BEGIN
p:= Pscal(LstN[j], Vun1); u:= 1 + p;
q:= Pscal(LstN[j], Vun2); v:= 1 + q;
r:= Pscal(LstN[j], Vun3); w:= 1 + r;
IF (u>v) THEN m:= u ELSE m:= v; IF (m<w) THEN m:= w;
IF (p<0) OR ((q<0) OR (r<0)) THEN s:= M1 / m
ELSE s:= M2 / m;
Px[1]:= Round(u * s); Px[2]:= Round(v * s);
Px[3]:= Round(w * s); L_C[j]:= Px
END
END;
PROCEDURE InitN(VAR L_N: Tab_Nf);
CONST g = 0.707106781187; // g = Rac(1/2)
h = 0.577350269190; // h = Rac(1/3)
Nf: Tab_Nf = ((x:1; y:0; z:0),
(x:0; y:1; z:0),
(x:0; y:0; z:1),
(x: g; y: g; z: 0), (x:-g; y: g; z: 0),
(x: 0; y: g; z: g), (x: 0; y:-g; z: g),
(x: g; y: 0; z: g), (x: g; y: 0; z:-g),
(x: h; y: h; z: h), (x:-h; y: h; z: h),
(x: h; y:-h; z: h), (x: h; y: h; z:-h));
BEGIN
L_N:= Nf
END;
(*HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH
Orientation spatiale du nouveau repère
HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH*)
CONST LambdaDeg = 10.0; PhiDeg = 25.0;
PROCEDURE Calc_U123(VAR U_1, U_2, U_3: Ve3D);
CONST DegRad = Pi / 180;
VAR Clam, Cphi, Slam, Sphi: Reel; W: Ve3D;
BEGIN
SinCos(LambdaDeg * DegRad, Slam, Clam);
SinCos(PhiDeg * DegRad, Sphi, Cphi);
W.x:= -Sphi; W.y:= Cphi; W.z:= 0; U_1:= W;
W.x:= - Slam * Cphi; W.y:= - Slam * Sphi; W.z:= Clam; U_2:= W;
W.x:= Clam * Cphi; W.y:= Clam * Sphi; W.z:= Slam; U_3:= W
END;
(*HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH
Programme principal
HHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHH*)
BEGIN
Copie_F1;
Calc_U123(Vun1, Vun2, Vun3);
InitF(LstF);
InitN(LstN);
InitC(LstC);
Calc_Mat_Im2(Larg_Image, Haut_Image, Matrice_2);
Creation_F2
END.
J'ai perdu beaucoup de temps dans la recherche de la meilleure (?) fonction retournant la couleur des faces en fonction de l'orientation de leur norme; il faut préserver les contrastes ainsi qu'un minimum de luminosité, mais c'est à la limite affaire de choix personnel.
Voici ce que l'on obtient pour diverses valeurs de la constante (M1) présente dans la procédure InitC(...):
M1 = 130, 160, 180, 200, 220, 240
Dernière modification par Wiwaxia (11-02-2021 21:47:53)
Hors ligne
#82 12-02-2021 10:29:21
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Des équations et des cubes
La proportion des faces sombres peut être modulée par l'intervention d'un critère beaucoup moins restrictif, en comparant la somme des 3 produits scalaires (S = p + q + r) à un seuil (Slim) dont on peut choisir la valeur.
PROCEDURE InitC(VAR L_C: Tab_Px);
CONST M1 = 50; M2 = 255.449; Slim = -0.100;
VAR j, k: Byte; m, p, q, r, s, t, u, v, w: Reel; Px: Pixel;
BEGIN
FOR j:= 1 TO Nf2 DO
BEGIN
p:= Pscal(LstN[j], Vun1); u:= 1 + p;
q:= Pscal(LstN[j], Vun2); v:= 1 + q;
r:= Pscal(LstN[j], Vun3); w:= 1 + r;
IF (u>v) THEN m:= u ELSE m:= v; IF (m<w) THEN m:= w;
s:= p + q; IncR(s, r);
IF (s<Slim) THEN t:= M1 / m
ELSE t:= M2 / m;
Px[1]:= Round(t * u); Px[2]:= Round(t * v);
Px[3]:= Round(t * w); L_C[j]:= Px
END
END;
Voici ce que l'on obtient en prenant M1 = 50 (afin que l'assombrissement soit marqué), et pour
M1 = -0.100, 0.000, 0.200, 0.300, 0.400, 0.700
J'avoue ne pas expliquer la persistance de la face claire, en bas à gauche; la représentation d'une sphère montrerait beaucoup mieux la répartition de l'éclairement.
Hors ligne
#83 12-02-2021 20:11:03
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Bonsoir Wiwaxia !
Lorsque je voulais représenter, justement cet objet, pour ne pas tracer les faces cachées, j'utilisai le produit scalaire d'un vecteur "de vue" avec les vecteurs normaux des faces. Lorsqu'il devenait >0, ou <0, selon sens du vecteur de vue, alors plus visible ...
Il me semble que pour l'intensité des couleurs, ça devrait fonctionner pareil : atténuation de l'intensité "proportionnelle" au produit scalaire ?
Avec modulation "entre 2 seuils" ajustables : très lumineux, peu lumineux ...
Mais cela dépend peut-être aussi de la définition des couleurs : mélanges de couleurs primaires ? Ou couleurs d'une palette ?
Ensuite ... dans ta présentation, je pense que tu traites les faces les unes après les autres, pas ensemble.
Alors la face jaune ? Et avec une sphère, pas facile je crois, il y a une infinité de facettes ...
Autre chose, le fait d'utiliser un vecteur "de vue", cela permet de changer la direction de venue de la lumière, et même d'envisager plusieurs sources différentes ! Ou de faire "tourner" l'objet ?
Voilà de quoi t'agiter les neurones ... bonne suite.
Et bonne soirée, Bernard-maths
Dernière modification par Bernard-maths (12-02-2021 20:17:32)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#84 13-02-2021 11:28:54
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Des équations et des cubes
Bonjour Bernard-maths,
Tu soulèves plusieurs questions relevant de la représentation des objets tridimensionnels.
... Lorsque je voulais représenter, justement cet objet, pour ne pas tracer les faces cachées, j'utilisai le produit scalaire d'un vecteur "de vue" avec les vecteurs normaux des faces. Lorsqu'il devenait >0, ou <0, selon sens du vecteur de vue, alors plus visible ...
C'est juste, mais ton critère n'intervient que lorsque l'on entreprend de ne représenter que les arêtes du polyèdre; si (Ni, Nj) désignent les normales aux faces adjacentes à l'arête considérée, le critère de visibilité de cette dernière est la vérification par les deux produits scalaires de la condition:
(Ni.OC) ≥ 0 OU (Nj.OC) ≥ 0 .
On a alors le choix entre une représentation "opaque", excluant le tracé des arêtes situées à l'arrière de l'objet, ou une représentation transparente ou semi-transparente liant le tracé des arêtes à la profondeur de leur milieu, donnée par le produit scalaire:
zkl = (OC.OIkl) = (1/2)(OC.(OAk + OAl)) ;
l'algorithme est dans ce cas relativement simple, et riche en diverses options.
L'avantage considérable du procédé que tu as initialement introduit est justement de dispenser le programmeur de l'identification et de l'inventaire les arêtes; il suffit alors de connaître l'orientation des normales aux faces, et les distances les séparant du centre.
De plus la détection de la face visible consiste à repérer l'endroit où la fonction caractéristique du polyèdre s'annule pour la première fois: ce qu'il peut y avoir derrière est alors dépourvu d'importance.
... Autre chose, le fait d'utiliser un vecteur "de vue", cela permet de changer la direction de venue de la lumière, et même d'envisager plusieurs sources différentes ! Ou de faire "tourner" l'objet ? ...
Tu as parfaitement raison sur ce point: je m'en suis résolument tenu à un polyèdre fixe dans le repère absolu (Oxyz), et à une perspzective à deux variables (λ, φ) définissant la position (C) de l'observateur et l'orientation du plan de l'image (u1, u2).
L'introduction des 3 produits scalaires dans la procédure de définition des couleurs InitC(...)
p:= Pscal(LstN[j], Vun1); u:= 1 + p;
q:= Pscal(LstN[j], Vun2); v:= 1 + q;
r:= Pscal(LstN[j], Vun3); w:= 1 + r;
... / ...
Px[1]:= Round(t * u); Px[2]:= Round(t * v);
Px[3]:= Round(t * w);
revient sommairement à considérer 3 projecteurs rouge, vert et bleu respectivement orientés selon les 3 directions (u1, u2, u3) du repère mobile.
J'aurais pu en effet envisager une ou plusieurs directions d'éclairage, distinctes de celle de la perspective, et simulant les effets physiques de diffusion et de réflexion de la lumière; mais l'on n'arrive à rien en abordant de front plusieurs problèmes difficiles, et le problème de géométrie analytique que tu as amené suffisait amplement.
La priorité revient à l'obtention d'un contraste satisfaisant au niveau des teintes et de la luminosité, afin de faire ressortir l'impression de profondeur.
... Alors la face jaune ? Et avec une sphère, pas facile je crois, il y a une infinité de facettes ...
Très simple au contraire, dans la mesure chaque point correspond à une face élémentaire d'orientation orthoradiale:
N(M) = (1/OM).OM .
La sphère permettrait de tester la qualité de l'éclairage, que je ne maîtrise pas très bien.
Hors ligne
#85 14-02-2021 10:14:17
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Salut Wiwaxia !
Bon, moi j'utilise GeoGebra, et quand je trace l'objet, ce sont des triangles ou quadrilatères qui sont tracés, selon leurs sommets, qui eux ont été "tournés". Alors la couleur est attribuée à la face, et je n'ai pas à la gérer.
Par contre je pourrais gérer l'intensité de la couleur, en jouant sur les 3 primaires et leurs intensités ...
Je te laisse continuer tes programmes, c'est toujours passionnant, mais je ne me suis pas encore remis à Pascal ...
A plus donc, Bernard-maths
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#86 17-02-2021 14:51:18
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Bonjour à tous !
Je vous ai promis un document expliquant comment générer un cube tronqué, et les équations associées ...
Alors voilà :
Avertissement : je reprends ici un document écrit en 2018, issu de mes expériences des années antérieures. J’applique ici une méthode de génération d’équations de polyèdres à partir d’un polyèdre donné, méthode qui consiste à tronquer le polyèdre de départ. Tous les polyèdres intermédiaires ont ainsi une équation « de surface », donc habituelle ...
Méthode : cette méthode consiste à partir d’une équation du polyèdre de départ considéré comme plein. C’est dire que cette équation concerne les points de la surface polyédrique, mais aussi de tout point intérieur !
Cette équation est de la forme S(d1,d2,d3,d4,d5,d6) = k > 0. C'est-à-dire, ici, Somme de 6 distances = un nombre k, (strictement) positif. On peut alors se poser la question : « mais où sont donc les points de l’espace (ici) qui seraient tels que S = k + d, d ≥ 0 ? ». La réponse donne une « surface de niveau d », comme je l’appelle.
Application : ici, le polyèdre de départ est un cube ABCDEFGH, dont les sommets ont pour coordonnées (±s ; ±s ; ±s).
Voir les différentes figures … La méthode ensuite fait glisser les sommets vers les milieux des 6 faces du cube de départ. Alors les faces rétrécissent en carrés, pour finir en 6 points, les centres des 6 faces. On a l’octaèdre dual du cube …
Ici s = 1, et le paramètre c, variant de 0 à s, permet de déplacer les sommets sur les faces, par exemple A se répartit en A1, A2 et A3 … MAIS on génère aussi des points intérieurs au cube A’, B’, C’ … H’. Ce qui donne un cube intérieur, homothétique de ABCDEFGH, dans le rapport (s-c)/s.
C’est de ce cube A’B’C’D’E’F’G’H’, qu’on va prendre une « équation pleine », puis générer une surface de niveau, dont les faces carrées (par 6 translations) seront les carrés intérieurs des 6 faces du cube ABCDEFGH !
Equation du cube plein :
Etant situé dans le cube, vous constatez que la distance entre 2 faces opposées est constante, égale au côté (arête). Entre les 3 paires de faces opposées, la somme des 6 distances vaut alors 3 côtés, donc ici : 3 (s+s) = 6s pour le cube ABCDEFGH, mais aussi : 3((s-c)+(s-c)) = 6(s-c).
Remarques :
Cette présentation n’est qu’un aspect de la « montagne de glace » (iceberg) qui se cache derrière ce type d’équation …
Non seulement la génération de polyèdres, mais aussi des arrondis sont possibles, ainsi que pour d’autres volumes …
La suite vous présente le document original de 2018 …
V est un curseur qui permet de voir tout ou partie de la figure, à tester !
Les 2 liens cjoint sont :
https://cjoint.com/c/KBrmHdGakNV
https://cjoint.com/c/KBrmMCT1BYV
Cordialement, bernard-maths
PS : je remarque qu'il y a une erreur sur les variations de c, non pas de 0 à s, MAIS de s à 0 !
Je vous laisse rectifier, eh eh ... (c-s) devient c ...
Dernière modification par Bernard-maths (17-02-2021 18:56:37)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#87 19-02-2021 15:00:19
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Hello !
Merci de me dire ce que vous pensez du dernier document !
Bernard-maths
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#88 23-02-2021 09:22:34
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Des équations et des cubes
Bonjour Bernard-maths,
... Merci de me dire ce que vous pensez du dernier document ...
Question très prosaïque: faut-il installer Geogobra ou l'une de ses applications pour ouvrir le fichier ggb, et dans l'affirmative laquelle ? Déjà il ne m'a pas été possible de consulter un précédent document au même format. Merci pour l'info.
Cordialement,
Wiwaxia.
Hors ligne
#89 23-02-2021 14:03:11
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Hello !
Personnellement j'ai installé GeoGebra sur mon ordi ... donc quand je clique sur le lien ci-dessous, je télécharge un fichier, qui se retrouve dans la barre des chargements, en bas (pour moi).
Si je clique sue le fichier chargé, il s'ouvre dans GeoGebra ...
Mais je ne sais pas ce qu'il se passe sur un ordi SANS GeoGebra !
Je vais essayer avec un ordi sans GeoGebra (si je peux !) ...
https://cjoint.com/doc/21_02/KBrmMCT1BY … -06-11.ggb
B-m.
BON ! Je viens d'essayer, et ça me demande avec quelle application ?
DONC il faut installer GeoGebra sur ton ordi, avant d'ouvrir le fichier chargé !!!
ALORS, pour des raisons d'interface, et côté pratique aussi, je préfère installer GeoGebra version 5, et non pas les suivantes !!!
Donc sur Google, je tape geogebra 5
on me propose :
https://www.google.fr/url?sa=t&rct=j&q= … uHCC3m0rui
Et j'ai un tableau de choix ; à droite en bas je choisis : GeoGebra Classique 5
GeoGebra gratuit et tout en un : géométrie, tableur, statistiques, calcul formel
Bon courage ... @ +
Dernière modification par Bernard-maths (23-02-2021 14:47:22)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#90 07-03-2021 18:24:29
- yoshi
- Modo Ferox
- Inscription : 20-11-2005
- Messages : 16 988
Re : Des équations et des cubes
Salut jeunesse,
Durant mon absence déménageuse, un de mes beaux-frères m'a fait découvrir un solide nommé "oloïde" ("inventé" par un certain Paul Schatz), qui ressemble à une moule...
https://www.youtube.com/watch?v=WNbcy5qAwHE
Ses équations (et plus encore) sont sur https://mathcurve.com/surfaces/orthobic … ycle.shtml
Après vous être bien amusés avec les cubes (et variantes) si vous ne connaissiez pas, vous devriez aimer...
@+
Arx Tarpeia Capitoli proxima...
Hors ligne
#91 08-03-2021 10:54:10
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Des équations et des cubes
Bonjour,
... Après vous être bien amusés avec les cubes (et variantes) si vous ne connaissiez pas, vous devriez aimer...
Cette information est en effet très intéressante, et mérite d'être commentée dans un discussion à part.
J'ai décroché des précédents échanges en raison d'obligations assez lourdes; il ne m'a pas été possible de suivre les développements multiples donnés au sujet initial. Cependant je m'efforcerai d'y répondre.
@ Bernard-maths: l'installation de Geogebra est d'une surprenante simplicité; je n'ai néanmoins pas eu directement accès au fichier en question.
Cependant l'application apparaît remarquable, et susceptible de rendre de précieux services dans l'élaboration rapide d'images mathématiques.
Hors ligne
#92 18-03-2021 09:47:36
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Des équations et des cubes
Bonjour,
Je réponds au message (#86) de Bernard-maths: tu exploites astucieusement une formule unique, qui conduit à une séquence de rhombicuboctaèdres dont les termes extrêmes (à faces d'aire nulle, réduites à un point) sont l'octaèdre et le cube.
Les 26 faces des polyèdres intermédiaires correspondent aux 33 = 27 combinaisons envisageables des domaines des coordonnées cartésiennes (x, y, z):
u < -1 ; -1 ≤ u ≤ 1 ; 1 < u ,
à l'exception de la combinaison centrale: -1 ≤ x, y et z ≤ 1
à laquelle se réduit le cas limite du cube.

L'inconvénient est qu'en renonçant à la démarche la plus générale, tu te restreins à une famille très particulière de polyèdres présentant simultanément des faces normales
# aux axes du repère (±1, 0, 0), (0, ±1, 0), (0, 0, ±1) ,
# à ses bissectrices (±a, ±a, 0), (±a, 0, ±a), (0, ±a, ±a) avec a = 1/√2 ,
# et à ses diagonales (±b, ±b, ±b) avec b = 1/√3 .
Tu exclus ainsi plusieurs polyèdres présentant des faces d'orientations semblables, mais en moindre nombre ou différemment éloignées du centre: cube et octaèdre tronqués, cuboctaèdre (tronqué ou non).
Voir Rhombicuboctaèdre, Polyèdres archimédiens.
https://mathcurve.com/polyedres/rhombic … edre.shtml
https://mathcurve.com/polyedres/archime … dien.shtml
Hors ligne
#93 18-03-2021 10:15:01
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Bonjour ! Toujours de beaux dessins ...
C'est tout à fait exact et j'en suis conscient, mais si pour le cube il y a 27 zones à étudier, pour d'autres (pas le tétraèdre, mais l'octaèdre ...) il y a beaucoup plus de cas !
J'ai voulu m'occuper de l'octaèdre : j'ai trouvé des formes "complexes", ça reste à poursuivre. Quant au tétraèdre je l'ai traité et je le reprend ... doucement !
Il y a pour moi 2 approches : celle utilisée pour le cube, mais il y en a une autre : elle consiste à partir d'une équation "pleine" de l'objet (ce qui semble toujours possible) et de chercher ce qu'il y a dehors à distance donnée ... J'appelle cela les surfaces de niveau.
Je pensais développer cette technique plus tard dans une autre conversation ? Et parler des autres polyèdres ...
Par un procédé de plusieurs homothéties combinées, on peut passer de la courbe de niveau au volume de départ qui se trouve tronqué !
Mais si tu veux des détails, je t'en donnerai ... puisque tu as trouvé "la faille" du cube.
Ce que je fait avec les figures rayonnantes, qui ouvre un grand champ de figures, permettra dans certains cas de retrouver des polyèdres tronqués ...
Alors, à plus, cordialement,
Bernard-maths
Dernière modification par Bernard-maths (18-03-2021 10:20:48)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#94 20-03-2021 13:16:05
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Des équations et des cubes
Bonjour,
Toujours à propos de ton message #86
Remarques :
Cette présentation n’est qu’un aspect de la « montagne de glace » (iceberg) qui se cache derrière ce type d’équation …
Non seulement la génération de polyèdres, mais aussi des arrondis sont possibles, ainsi que pour d’autres volumes ...
On peut effectivement les obtenir en remplaçant la somme (|1 + u| + |1 - u|)
par le terme T = (1 + uN)1/N;
le calcul du vecteur gradient ne pose pas de difficulté, puisque l'on a (dT/du) = uN-1/(1 + u)(N-1)/N .
Voici ce que l'on obtient pour le même polyèdre, en prenant N = 8 :
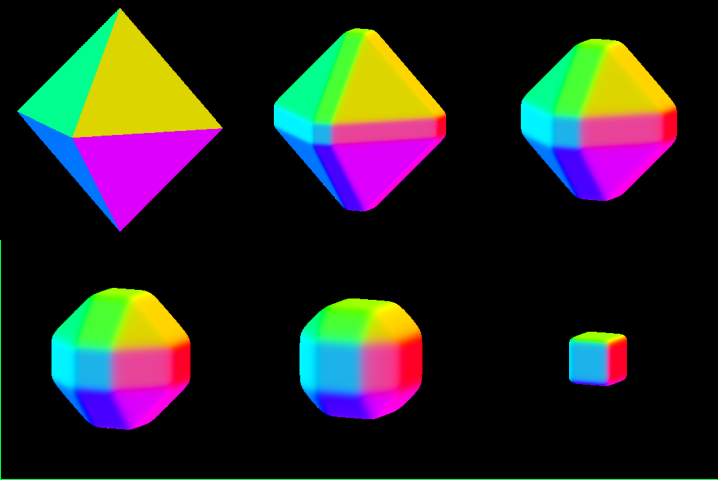
Il faut que l'exposant (N) soit suffisamment élevé afin de réduire la largeur des plages intermédiaires; les calculs les plus rapides s'obtiennent pour N = 2k ou 2k + 2 .
Hors ligne
#95 20-03-2021 14:22:03
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Bonjour Wiwaxia !
Alors un peu de temps le W-E ?
Dans les arrondis, je pense qu'on peut aussi utiliser un exposant de ]0;1] ...
MAIS je suis complètement coincé par le possibilités restreintes de GeoGebra en 3D, je suis obligé de faire des montages de figures ...
TON logiciel (ou un autre) est-il capable de "prendre une équation" et de tracer la figure correspondante ?
Je pense (entre autre) à Pov Ray, ... qui est payant, mais je ne peux pas me lancer "pour rien" si c'est pas efficace.
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#96 20-03-2021 14:22:16
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Bonjour Wiwaxia !
Alors un peu de temps le W-E ?
Dans les arrondis, je pense que tu peux aussi utiliser un exposant de ]0;1] ... donnant du "rentrant", ça change un peu ...
MAIS je suis complètement coincé par les possibilités restreintes de GeoGebra en 3D, je suis obligé de faire des montages de figures ... ce qui permet de mettre de la couleur selon les types de forme.
TON logiciel (ou un autre) est-il capable de "prendre une équation" et de tracer la figure correspondante ?
Je pense (entre autre) à Pov Ray, ... qui est payant, mais je ne peux pas me lancer "pour rien" si c'est pas efficace.
A bientôt, Bernard-maths
Dernière modification par Bernard-maths (20-03-2021 14:29:01)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#97 20-03-2021 15:58:49
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
@ Wiwaxia,
pour tes derniers dessins, je remarque que ça ne correspond pas à ce que j'obtiens théoriquement !?
Tes dessins donnent des arrondis sur les arêtes, alors que moi je garde les 8 triangles, mais entre les triangles je n'ai pas de plats mais des morceaux de cylindres, et aux sommets j'ai des calottes sphériques ... si n > 1, ou rentrés si n < 1. Comme pour un dé à jouer.
Je vais essayer de te faire un dessin (en cours, mais en plan pour le moment ...)
B-m
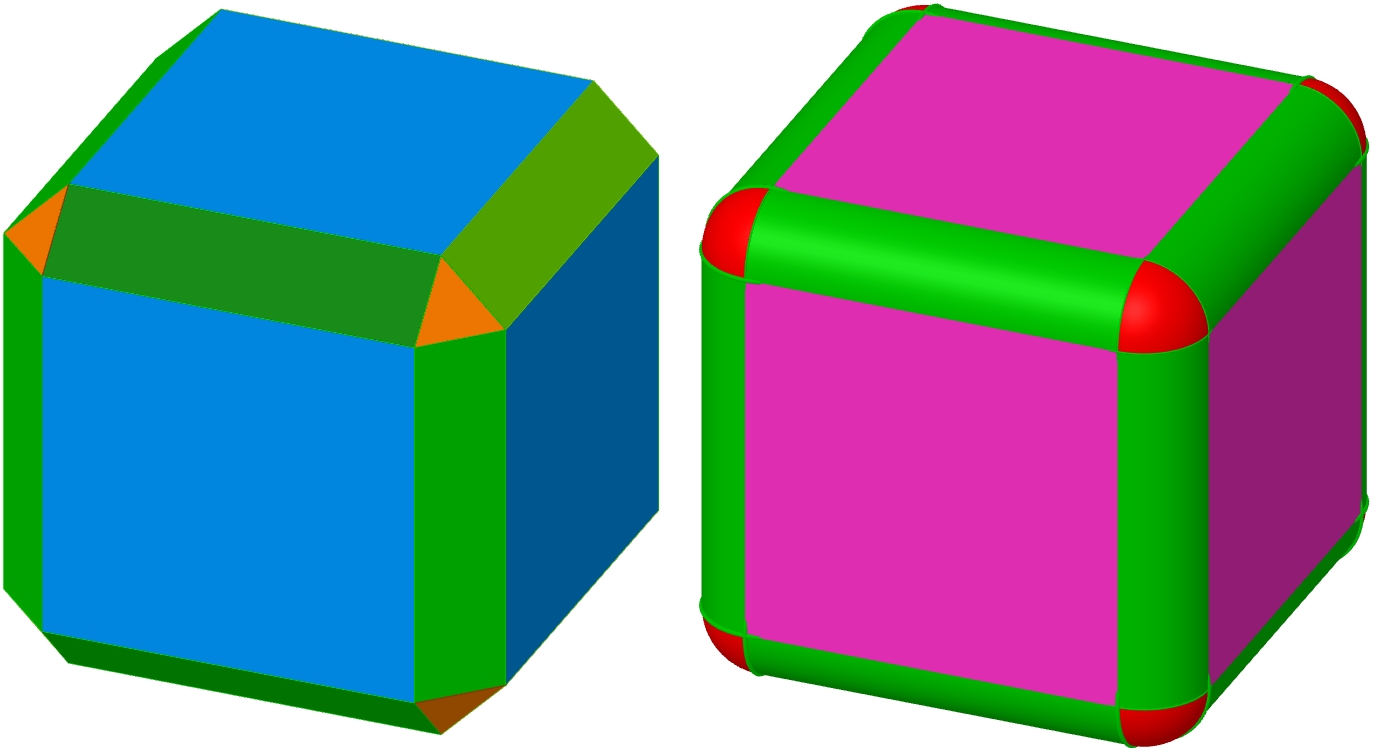
Comme sur ces figure : gauche pour n = 1, droite pour n =3.1 environ, figure approchée !
Dernière modification par Bernard-maths (20-03-2021 17:08:17)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#98 22-03-2021 11:31:01
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Des équations et des cubes
Bonjour Bernard-maths,
... pour tes derniers dessins, je remarque que ça ne correspond pas à ce que j'obtiens théoriquement !?
Tes dessins donnent des arrondis sur les arêtes, alors que moi je garde les 8 triangles, mais entre les triangles je n'ai pas de plats mais des morceaux de cylindres, et aux sommets j'ai des calottes sphériques ... si n > 1, ou rentrés si n < 1. Comme pour un dé à jouer ...
La dernière série de surfaces fermées est aux précédentes
ce que le graphe d'équation x8 + y8 = 1 est au carré (1)
et ce que la surface d'équation x8 + y8 + z8 = 1 est au cube (2):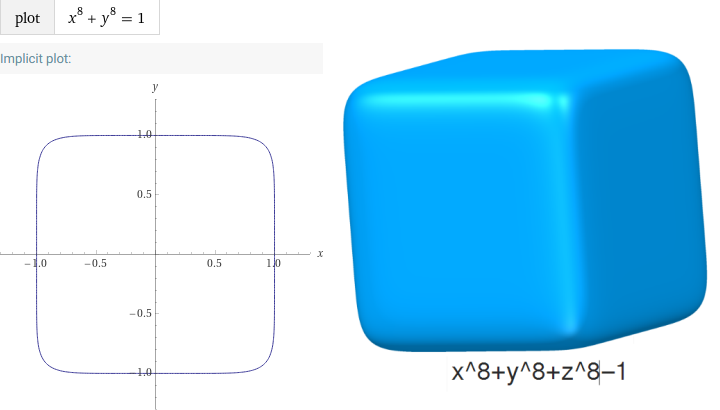
(1): image réalisée sur WolframAlpha.
(2): image réalisée sur Surfer
Il n'y a pas de délimitation précise des arrondis, et si les dimensions d'une face se réduisent en ordre de grandeur à la largeur des précédents, alors cette face ne présente plus de méplat.
L'inconvénient de ta démarche est son défaut de généralité; elle ne vaut que pour une famille de polyèdres.
Les surfaces représentées dans le message (#94) dérivent de la même équation
(aN + xN)1/N + (aN + yN)1/N + (aN + zN)1/N = b .
... TON logiciel (ou un autre) est-il capable de "prendre une équation" et de tracer la figure correspondante ? ...
Le programme que j'ai fait admet en théorie toute équation du type F(x, y, z) = 0 ... à condition qu'elle ne soit pas trop lourde, de même que les composantes du gradient. Sous ce rapport, l'oloïde signalé par Yoshi présente une complexité (pour l'instant) incontournable: j'ai tenté en vain de simplifier l'équation cartésienne pour envisager un temps de calcul raisonnable.
... Je pense (entre autre) à Pov Ray, ... qui est payant, mais je ne peux pas me lancer "pour rien" si c'est pas efficace ...
La dernière version de POV-Ray est gratuite, et après une période de familiarisation assez laborieuse, j'ai pu obtenir une série de polyèdres conçus comme un réseau d'arêtes, à l'aide seulement de deux sortes d'objets (sphères et cylindres).
Je viens de retrouver l'un des polyèdres permutationnels réalisés à l'aide de ce logiciel:

Dernière modification par Wiwaxia (22-03-2021 16:44:48)
Hors ligne
#99 22-03-2021 12:43:20
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Des équations et des cubes
Bonjour Wiwaxia !
je crois qu'il faut qu'on mette les choses au point ... nous travaillons sur des équations différentes.
Je connais ces équations en puissances, que j'appelle de super-cube, et qui donne des formes arrondies sans plat.
Je vais donc lancer une nouvelle discussion sur les équations de polyèdres convexes pleins, et les surfaces de niveau qu'on peut en tirer ...
Je t'en avais déjà parlé, et tu verras que ça mène à des approches différentes ! Qu'en penses tu ???
J'ai besoin pour cela de me "réviser" les étapes, et cette semaine, je suis en sessions d'animations pour la quinzaine de "les maths en scène".
Il faut aussi que je te donne 2 équations pour voir si tu les sors correctement avec tes logiciels, ou si tu fais "du montage" comme moi avec GeoGebra!?
Voilà bien du sport en perspective !!!
Cordialement, Bernard-maths
Dernière modification par Bernard-maths (22-03-2021 13:07:32)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#100 24-03-2021 11:01:09
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Des équations et des cubes
Bonjour,
... Il faut aussi que je te donne 2 équations pour voir si tu les sors correctement avec tes logiciels, ou si tu fais "du montage" comme moi avec GeoGebra!? ...
J'ai déjà donné mon accord de principe pour des équations de complexité raisonnable.
J'exprime cependant ma réserve dans le cas d'un usage immodéré des valeurs absolues, pour lesquelles tu manifestes un intérêt hors du commun: la prolifération des cas particuliers risque de conduire à une situation ingérable, en ce qui concerne la dérivation.
Ceci dit, la discussion reste ouverte.
... je crois qu'il faut qu'on mette les choses au point ... nous travaillons sur des équations différentes.
... / ...
Je vais donc lancer une nouvelle discussion sur les équations de polyèdres convexes pleins, et les surfaces de niveau qu'on peut en tirer ...
Soit un plan (P), et (H) le pied de la perpendiculaire abaissée sur celui-ci depuis une origine donnée (O).
Ce plan est séparé du point (O) par la distance au centre Dc = OH ;
son orientation spatiale est définie par le vecteur unitaire (un) colinéaire à (OH) et de même sens:
un = (1/OH).OH .
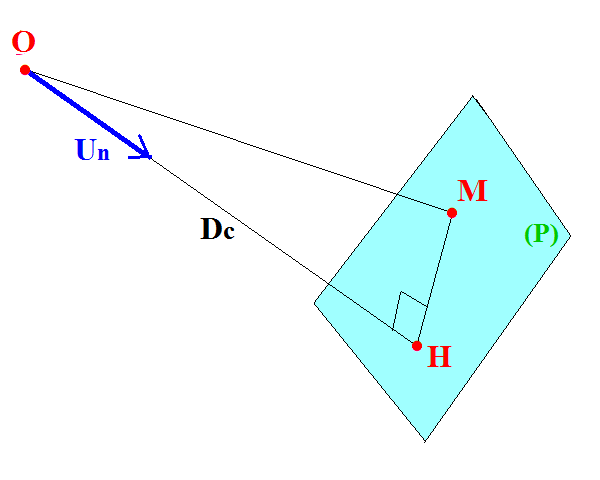
On a pour tout point (M) du plan considéré HM perpendiculaire à un,
ce qui se traduit par l'annulation du produit scalaire correspondant: un.HM = 0 ;
en tenant compte de ce que HM = OM - OH ,
et en posant p = un.OM , il vient:
p - un.OH = 0 = p - (OH)(un.un) ,
soit finalement: p - Dc = 0 .
Soit maintenant un point quelconque (M) et la fonction F(p) = p - Dc + |p - Dc| ;
son expression dépend de la position du point par rapport au plan d'équation p = Dc :
a) si p ≤ Dc , alors F(p) = p - Dc + (Dc - p) = 0 ;
b) si p > Dc , alors F(p) = 2(p - Dc) > 0 .
Deux régions de l'espace, séparées par le plan frontière d'équation p = Dc , sont par conséquent discernables:
a) celle qui contient l'origine, caractérisée (comme le plan limite) par l'égalité F(p) = 0 ;
b) l'autre pour laquelle on a F(p) > 0 .
Élargissons désormais la notion précédente au cas d'un polyèdre convexe, défini par la donnée d'au moins 4 plans entourant l'origine, en considérant la somme suivante étendue à toutes les faces présentes dont chacune est caractérisée par le couple (unj , Dcj):
S(M) = Σj=1Nf (Fj(p)) ;
Le domaine intérieur (faces incluses) du polyèdre est caractérisé par l'égalité S(M) = 0 ;
comme il n'intervient en effet que des termes non-négatifs, chacun d'eux est obligatoirement nul:
Fj(p) = 0 ;
on définit ainsi l'intersection commune à tous les demi-espaces délimités par les diverses faces, et contenant l'origine.
Remarques:
# La donnée des sommets n'est pas indispensable: il suffit simplement de connaître pour chaque face la distance (Dcj) la séparant du centre, et les composantes du vecteur unitaire normal (unj) correspondant.
# La présence d'un centre de symétrie n'est pas nécessaire; s'il existe toutefois, l'expression de la somme S(M) se simplifie par regroupement des termes, dont le nombre est divisé par deux; on retrouve alors une expression du type:
S(M) = Σ (|Dc + p| + |Dc - p|) .
Dernière modification par Wiwaxia (28-03-2021 20:11:38)
Hors ligne








