Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
#26 25-04-2021 20:48:17
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
bonsoir,
pour l'image, il s'agit d'un puzzle sur
Sur le programme GeoGebra, j'ai fait un assemblage, car en 3D GeoGebra ne sait pas "lire" les équations (en général);
mais l'objet répond à une équation !
Dernière modification par Bernard-maths (25-04-2021 20:49:40)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#27 26-04-2021 13:26:29
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour à tous !
je ne vais pas m'éterniser sur mes dernière figures, en #22, si un matheux veut des précisions, je verrai avec lui pour des détails.
Ces détails sont un peu délicats à mettre à jour, alors ...
Je vais passer à quelques "principes" ou "méthodes" pour engendre des objets rayonnants.
Le 1er principe (si on peut dire), c'est de mettre un obet dans un autre, puis de faire grandir celui qui est dedans, jusqu'à ce qu'il atteigne son "enveloppe", puis qu'il déborde !
ALORS, déjà en chaque position de contact, en chaque point de contact on peut tracer une droite "rayon", puis lorsque ça déborde, on a une figure d'intersection des 2 objets initiaux, alors on trace un tube ayant cette intersection pour base ...
Je vais illustrer ça avec les 4 figures suivantes :
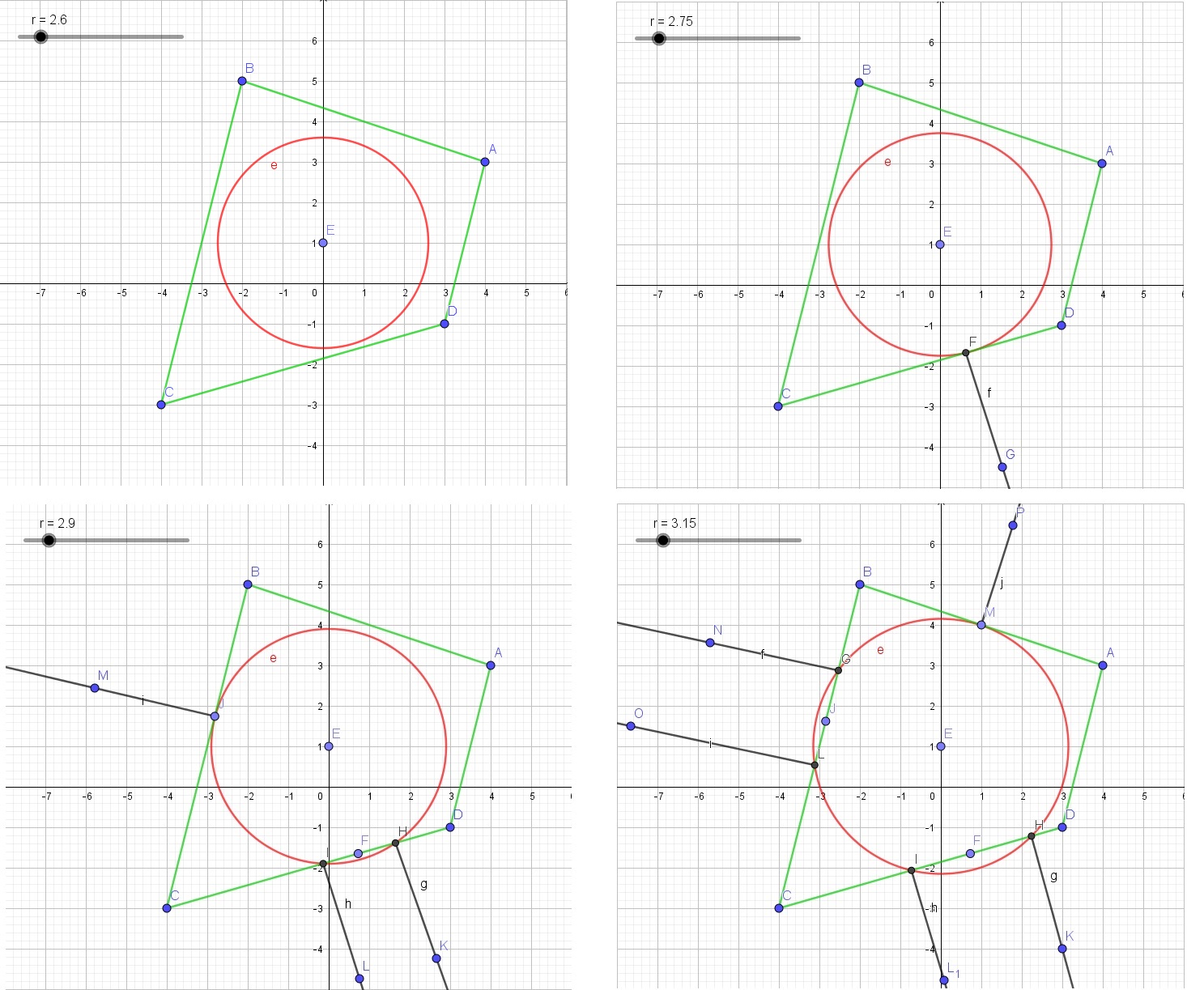
On voit :en fig1 un quadrilatère ABCD vert avec un cercle rouge à l'intérieur. En fig2, r = 2.75, le cercle devient tangent en F au côté [CD], alors apparaît un rayon [FG) sous forme de demie droite ...
En fig3, r = 2.9, le cercle devient tangent en J au côté [BC], alors apparaît un rayon [JM) sous forme de demie droite. MAIS le rayon précédent s'est élargi ! Il est limité par les 2 demies droites [HK) et [IL) ...
Puis en fig4, les 2 premiers rayons s'élargissent encore, et pour r = 3.15, un autre rayon [MP) apparaît sur le côté [AB] ... etc ...
Le 2ème principe (si on peut dire), c'est de choisir comment va se comporter le rayon qui apparaît !
J'ai choisi de le voir sortir perpendiculairement au côté, comme mes 1ères équations le font, MAIS rien ne vous oblige à faire ça, en dehors de toute équation ! L'ARTISTE est libre ...
Du coup je n'ose plus parler de principe ... Mais de "conseils" peut-être ?
ALORS quand la figure intérieur a bien grandi, elle risque d'englober l'autre ... du coup les rôles sont inversés, et c'est le contraire !
Voici un petit dessin en 3D ...
Dernière modification par Bernard-maths (26-04-2021 14:48:11)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#28 27-04-2021 17:19:06
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour à tous !
J'ai été interrompu, et j'ai laissé des fautes de frappe ! Vous aurez corrigé j'espère.
Je vais maintenant vous laisser quelques exemples, et programmes, de rayonnements en 3D.
https://cjoint.com/c/KDBprzoZ1if
https://cjoint.com/doc/21_04/KDBprzoZ1i … -04-26.ggb
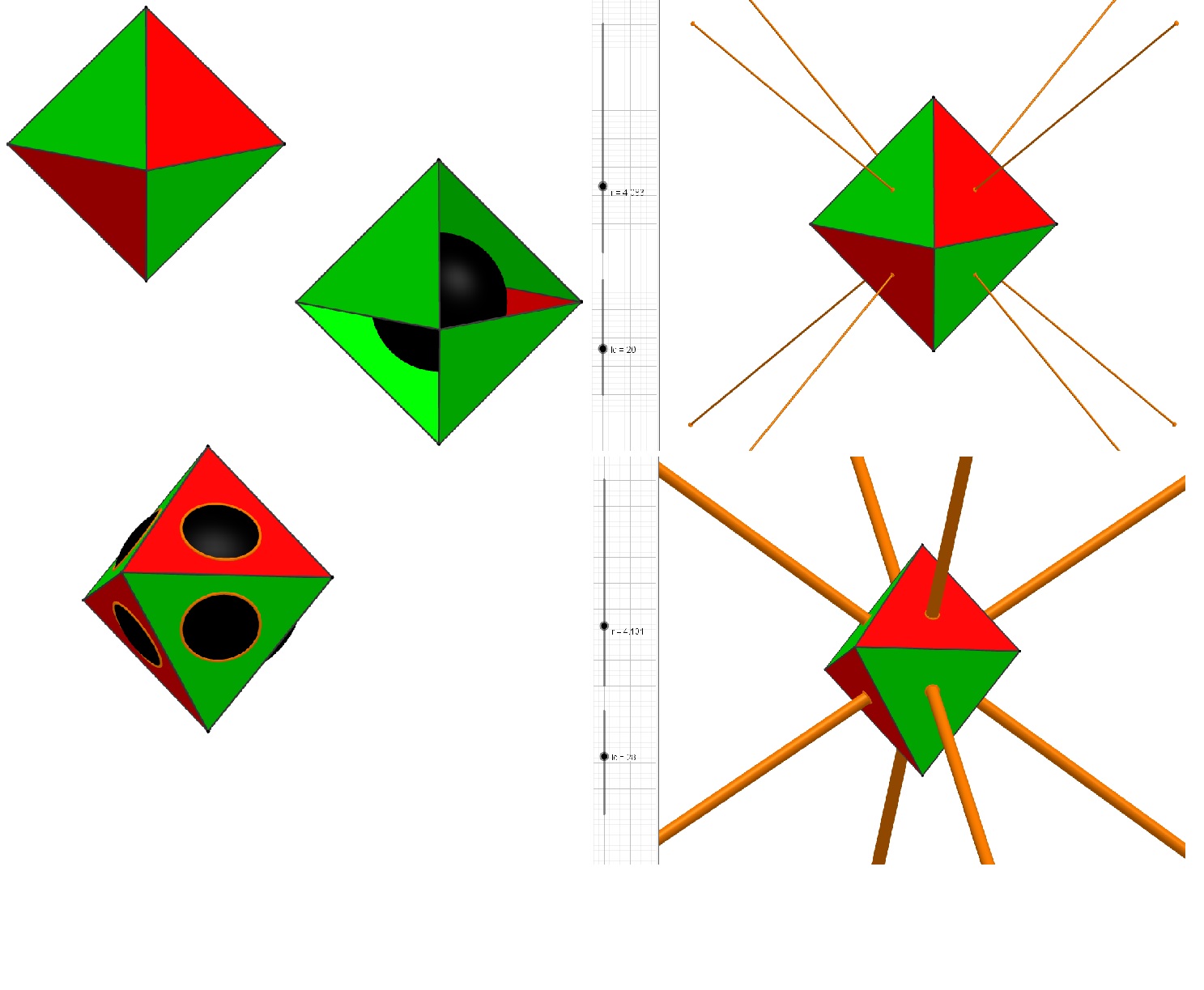
Voilà le 1er exemple : on y présente à gauche un tétraèdre rouge et vert, contenant une sphère noire, susceptible de déborder, selon les cercles oranges. A droite vous voyez 2 cas de rayonnements, r = 4.083 est le début (1ère valeur de r), en-dessous, r est plus grand ...
Si vous chargez le programme, en jouant sur le curseur de r vous verrez que ça peut grandir et déborder même !
Le 2ème curseur, lc, règle la longueur des rayons ...
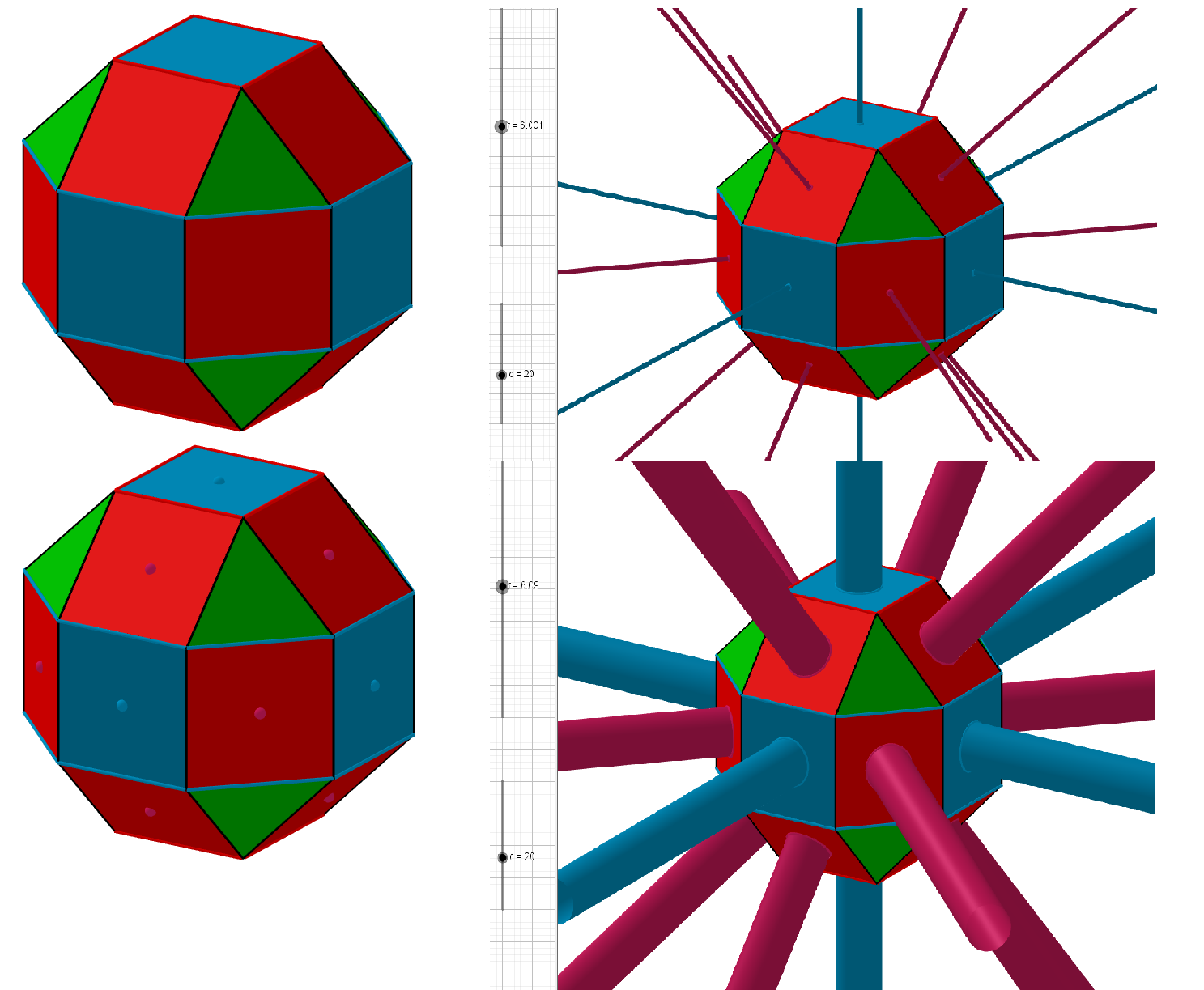
Passons au 2ème exemple : il s'agit d'un rhombicuboctaèdre (voir mathcurve.com), avec une sphère intérieure.
https://mathcurve.com/polyedres/rhombic … edre.shtml
https://cjoint.com/c/KDBpS5pkYff
https://cjoint.com/doc/21_04/KDBpS5pkYf … -04-26.ggb
Si vous chargez le programme, le rayonnement ne commence que pour r = 6, on voit des points apparaître, r= 6.01 ça commence les rayons, r > 6.01, les rayons grossissent. C'est pas fini !
Suite : Si r augmente les rayons grossissent. MAIS les faces triangulaires ont plus éloignées du centre que les faces carrées ! Alors les rayons des triangles apparaissent plus tard.

Puis continuent de grossir jusqu'à être tangents aux côtés des carrés et triangles. Puis se débordent les uns sur les autres, et puis le rhombicuboctaèdre disparaît ! ... etc ...
Il s'agit d'un dessin, quand est-ce que la "réalité géométrique" fait place à "l'artiste" ?
Il est possible d'écrire une équation engendrant ces rayons (je ne l'ai pas fait, la flemme ...), assez complexe (?), et son étude pourrait nous éclairer ...
Bon, j'arrête pour ce soir. Désormais, sauf demandes explicites, je continuerai de temps en temps à alimenter cette discussion, avec d'autres exemples variés, et plutôt "artistiques".
Bonne soirée, Bernard-maths
Dernière modification par Bernard-maths (27-04-2021 18:29:38)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#29 04-05-2021 10:43:53
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour à tous !
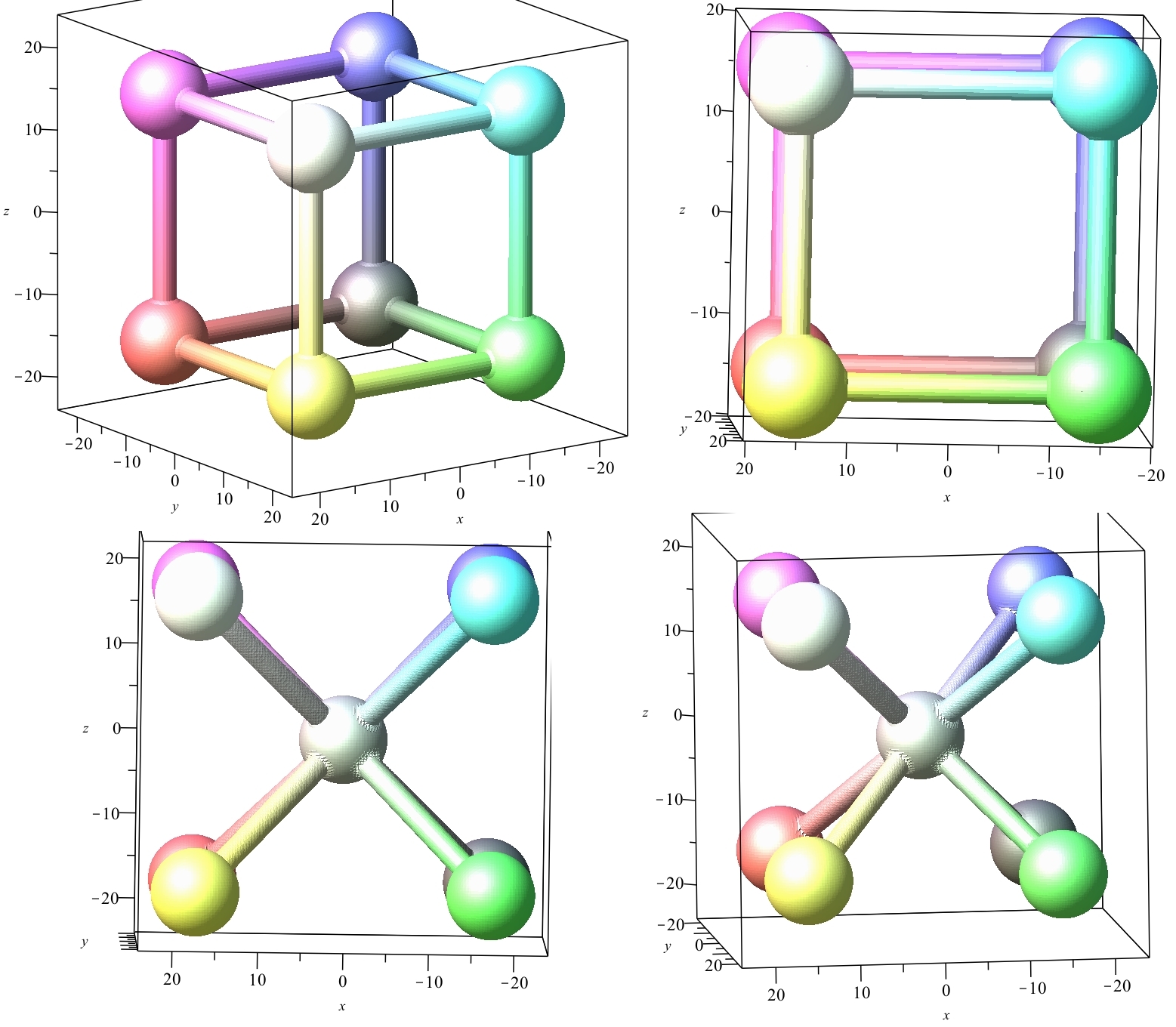
Je vous ai présenté en #21 des figures rayonnantes en 3D, avec les sphères.
Si vous connaissez l'Atomium de Bruxelles, vous pouvez constater que cette figure en représente les 8 sphères périphériques, reliées par les 12 tubes cylindriques. Alors, que manque-t-il pour compléter cet Atomium ?
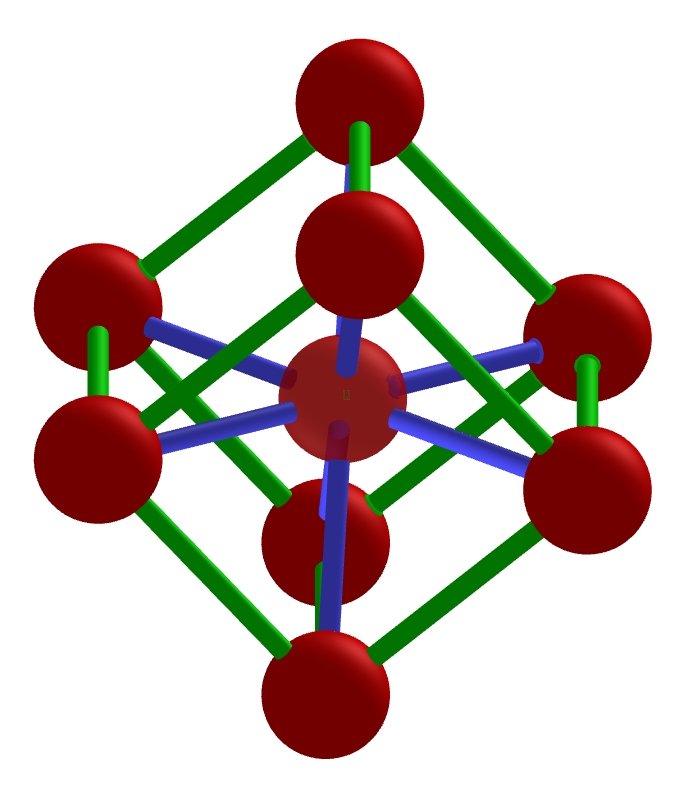
https://cjoint.com/doc/21_05/KEeiPy67yO … 018-08.jpg
La figure doit vous inspirer ... quelles méthodes pensez-vous pouvoir utiliser ?
Je vous laisse chercher, je repasserai bientôt pour vous proposer des manipulations !
@+, Bernard-maths
BIENTÔT est arrivé !!! Nous sommes le 02-05-2022, donc 1 an - 2 jours plus tard ... :-))
Je vous propose de suivre l'aventure en #34 et suivante(s) --->
Bernard-maths
Dernière modification par Bernard-maths (04-05-2022 07:26:15)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#30 14-05-2021 15:10:27
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour aux curieux !
Bon, je suis occupé sur plusieurs postes ! Donc je ne peux pas revenir "bientôt" ...
Alors je vais vous donner mon idée : je prends la boule du milieu et une des 8 boules. Je prends le centre de symétrie des 2 boules, et je crée l'effet de rayon entre ces 2 boules. ll reste à dupliquer cet effet en utilisant les symétries par apport aux 3 plans du repère, avec abs(x), abs(y) et abs(z) à la place des x, y et z de la formule obtenue ...On obtient alors la boule centrale avec les 8 boules, reliées par les cylindres "obliques".
En superposant les 2 figures, aux niveaux des 8 boules, on obtient la figure présentée.
Je ne l'ai pas encore fait en 3D, mais seulement en 2D ... Donc il faudra patienter ... "un peu" !
Cordialement, Bernard-maths
Dernière modification par Bernard-maths (14-05-2021 15:12:48)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#31 13-06-2021 20:46:01
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonsoir à tous !
J'ai été très occupé ces derniers temps, mais j'ai aussi bien réfléchi ! En plus, je me suis procuré le logiciel , qui, entre autres, permet de reproduire en 3D des figures par leurs équations, c'est un vrai plaisir !
Dans les discussions #16 et #21, je vous ai montré quelques variations sur des formules rayonnantes. Je vais vous indiquer ici la formule utilisée avec , et vous donner 4 exemples de figures évolutives.
En #15, je vous donnais la formule 2D : eq5 : (abs(xsi(abs(x))))^n + (abs(ysi(abs(y))))^n = r^n ..., qui devient en 3D :
abs(abs(abs(x) - x0 + a) + abs(x) - x0 - a)^n + abs(abs(abs(y) - y0 + a) + abs(y) - y0 - a)^n + abs(abs(abs(z) - z0 + a) + abs(z) - z0 - a)^n = (2*r)^n
La figure dépend d'un certain nombre de paramètres ... d'abord le point Oméga(x0;y0;z0), qui fixe l'aspect général de la figure, qui se développe autour des 8 sommets d'un parallélépipède rectangle, et la variable r, qui permet le développement autour des sommets, puis le long des 12 arêtes, et fixe les dimensions à : 2(x0+r), 2(y0+r), et 2(z0+r).
Puis l'exposant n qui donne la forme générale à chaque partie située à un sommet. Et aussi a qui règle la limite du rayonnement autour des 8 sommets.
Alors voici le "programme", à recopier avec soin sur "maple" :
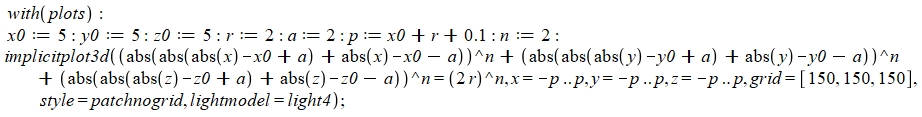
Et puis 4 "cinémas" de 6 figures.
Première série : des astroïdoctaèdres.
Deuxième série des octaèdres.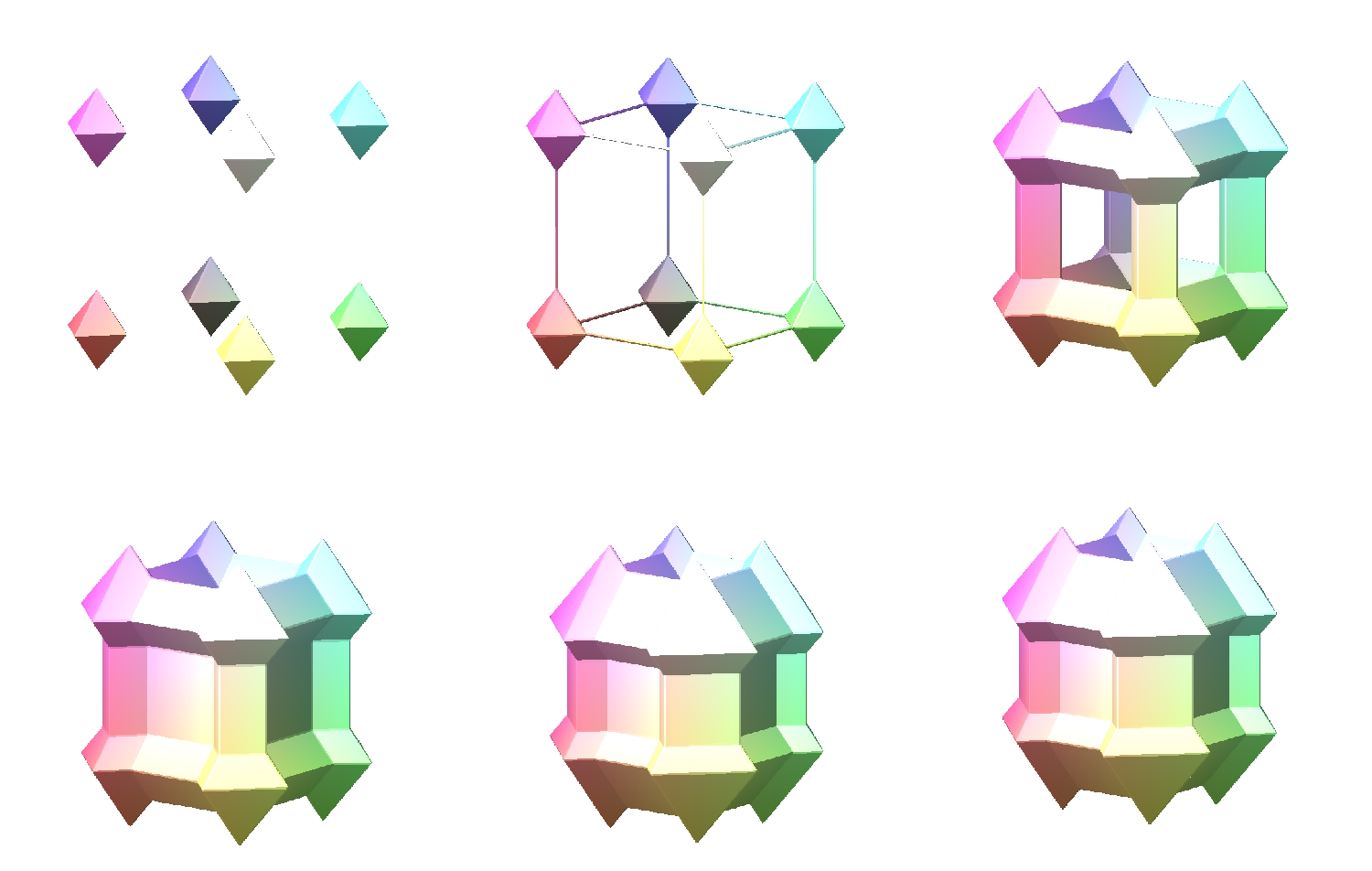
Troisième série des sphères.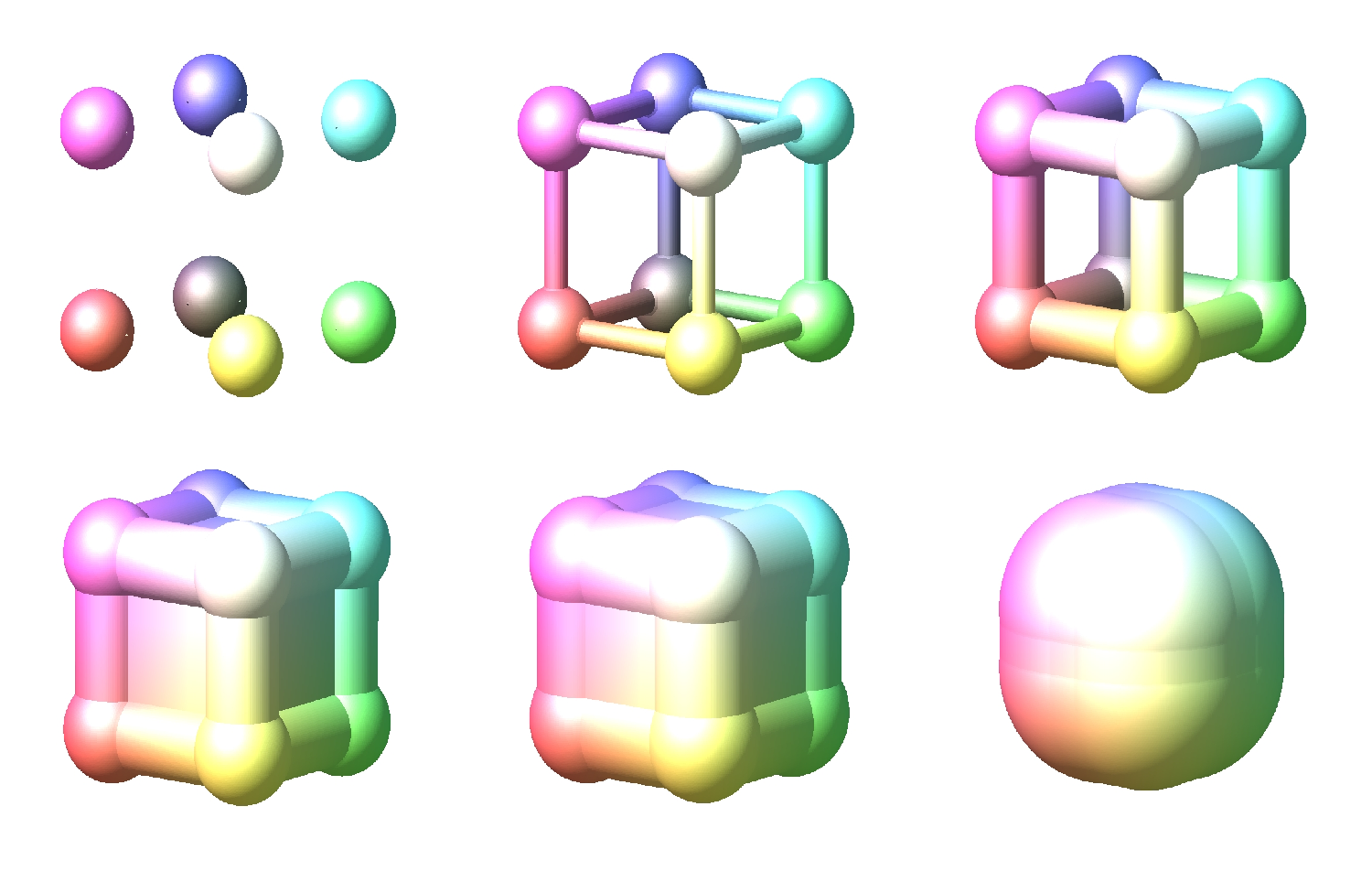
Quatrième série des drôles de cubes.
Alors, comment ça marche ?
La 1ère figure est tracée pour r <= a. On obtient la figure de bas aux 8 sommets. Puis r dépasse "un peu" la valeur de a ... on voit apparaître des liaisons le long des arêtes. Les liaisons s'épaississent ... jusqu'à apparition (4ème figure) de plan qui bouchent les côtés !
Puis la figure grandit, et a tendance à faire une sorte de "boule". Voilà !
Plus tard je vous parlerai des variantes, nombreuses.
Bernard-maths
Dernière modification par Bernard-maths (13-06-2021 21:49:22)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#32 25-04-2022 15:17:05
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour à Wwaxia ! ... Bonjour les Autres ...
Il y a un an et un jour, tu me posais une question en #22, et je répondais en #23 ...
J'avais oublié que j'avais déjà bidouillé des bras variables en février 2019 !!!
Mais c'était pas beau aux frontières, et j'avais laissé tomber. Je viens de reprendre un peu, et j'ai éliminé les bavures aux frontières.
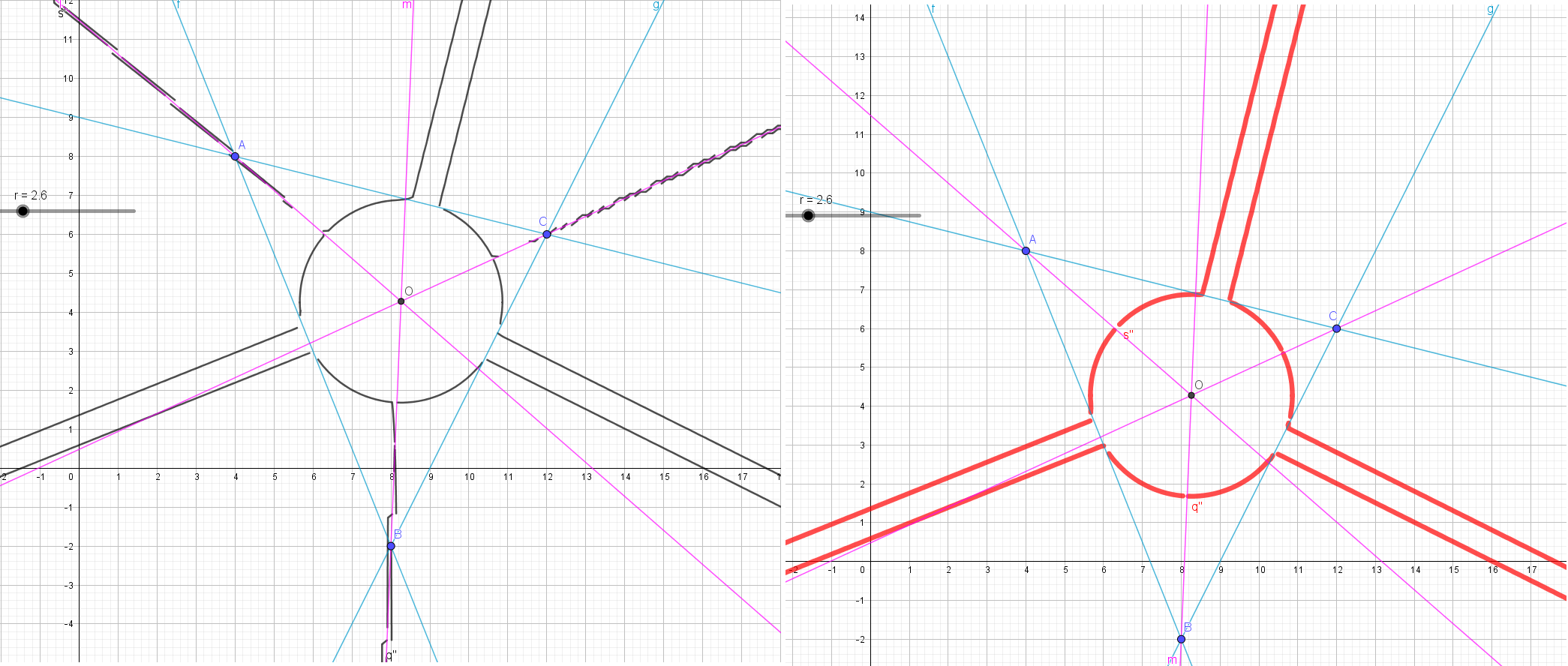
Le principe consiste à prendre un polygone autour d'un cercle inscrit ; les points de contact étant variables sur le cercle, le polygone est déformable. En gérant un 2ème cercle concentrique de rayon variable, on engendre les bras par dépassement des côtés. On limite chaque zone de bras par des fonctions "indicatrices" des zones ...
Il faut que je reprenne tranquillement les équations, et que je teste avec Maple !
Voici ce que ça peut donner en 3D, ici avec 4 points. On n'est pas obligé d'avoir un polygone ou un polyèdre !!!
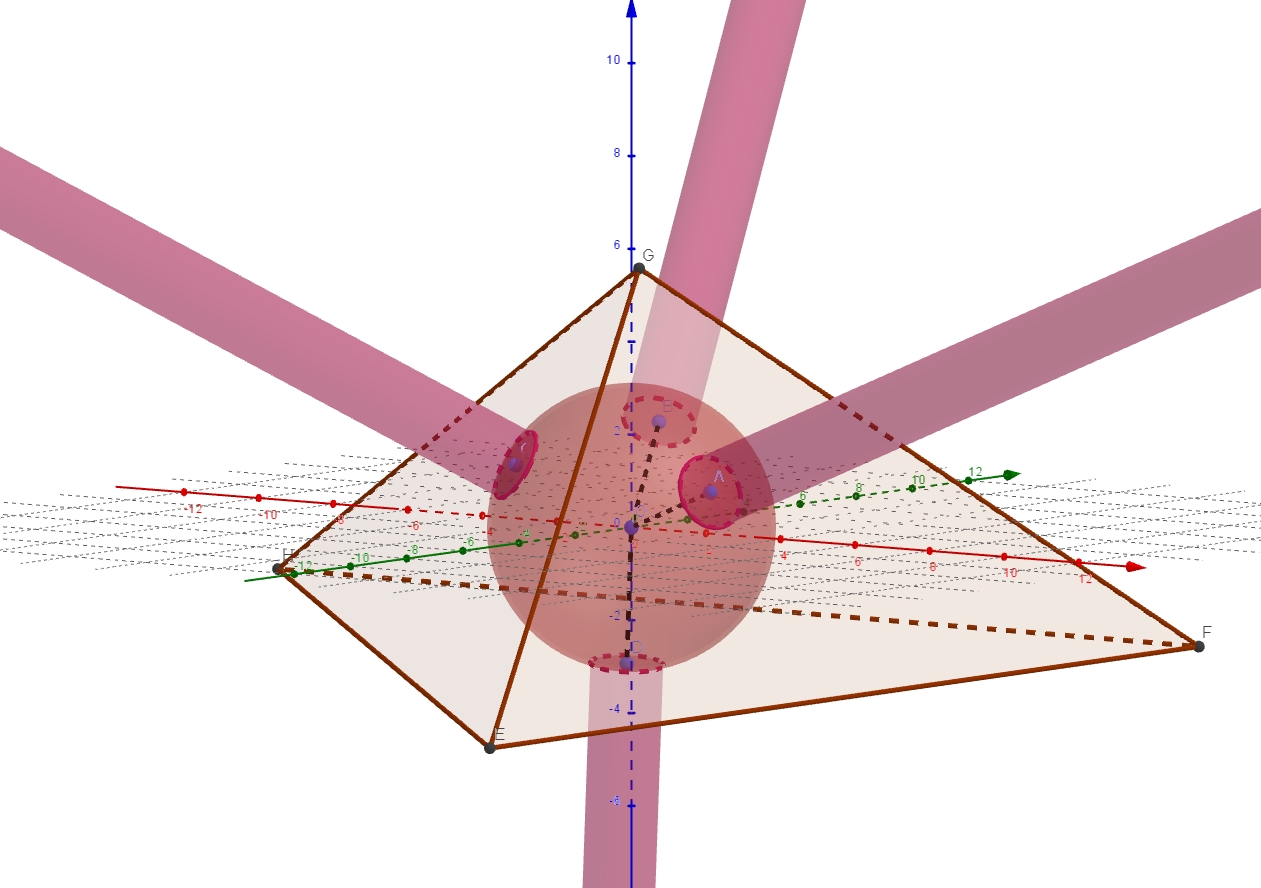
Voilà encore de quoi s'amuser un peu ...
Bernard-maths
Dernière modification par Bernard-maths (25-04-2022 16:10:05)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#33 25-04-2022 16:58:30
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour Bernard-maths,
Certaines de tes figures retiennent mon attention, en raison de leur aptitude à représenter les réseaux atomiques présents à l'état solide.
Elles s'apparentent aux images que donne le logiciel Jmol, qui utilise Java et impose des contraintes liées à la représentation des atomes des divers éléments.
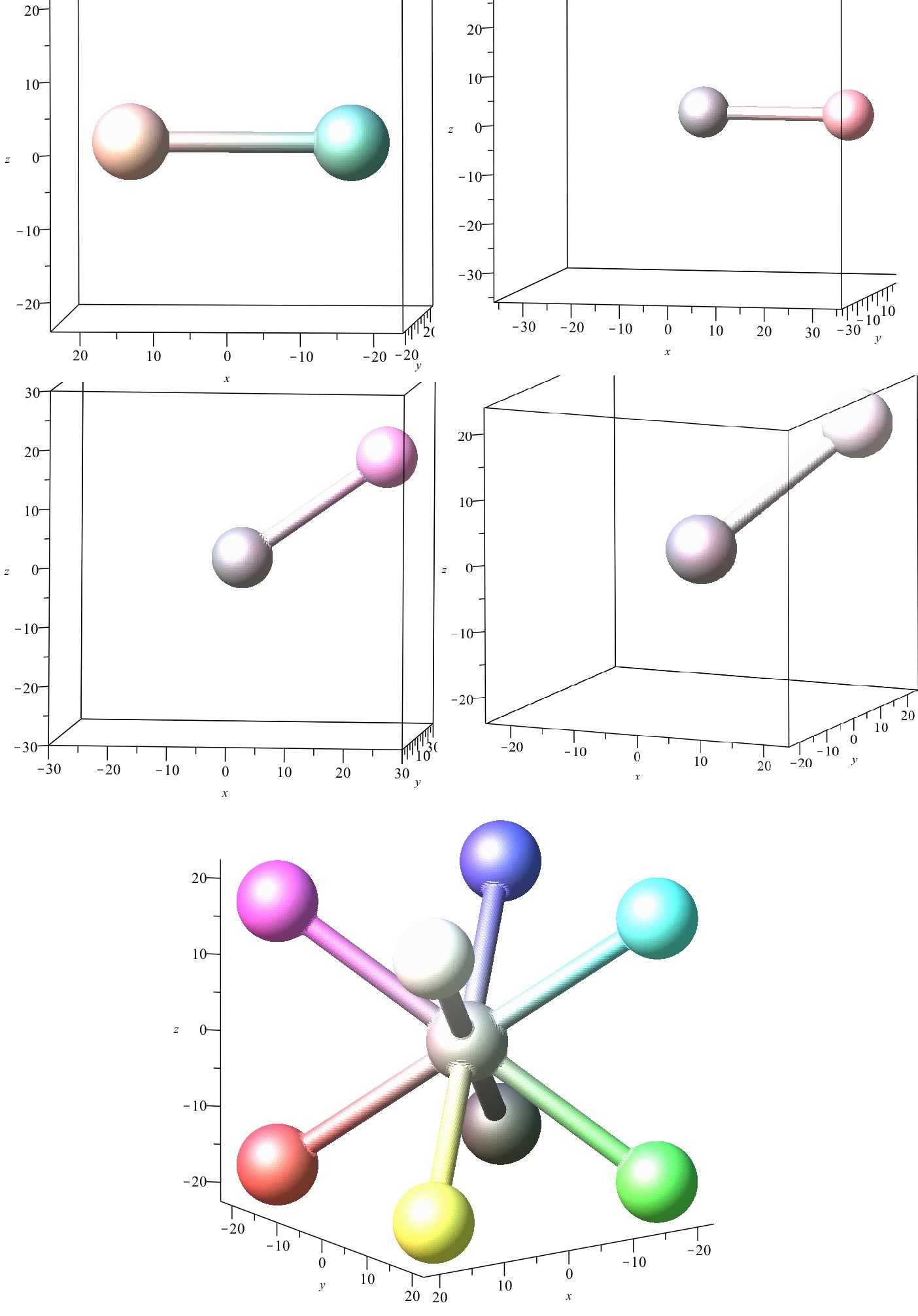
Les deux exemples donnent une idée de l'étendue de la complexité des structures que l'on peut rencontrer - il s'agit ici des formes (VII) et (VI) du silicium, que l'on rencontre sous des pressions dépassant 40 GPa; et je m'en suis volontairement tenu aux structures homoatomiques ...
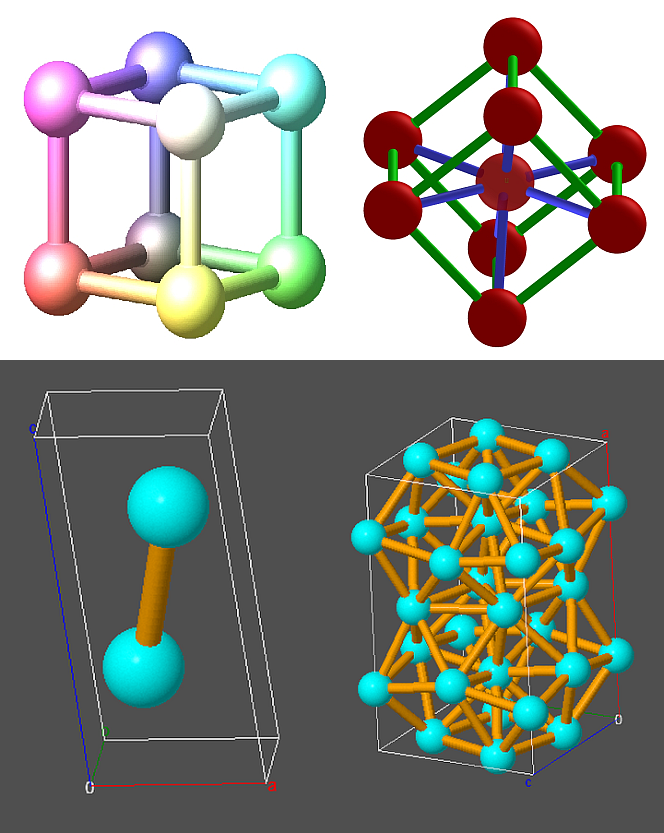
je ne connais que POV-Ray, comme logiciel capable de rivaliser avec Jmol, et d'une façon beaucoup moins souple.
Les curieux pourront activer le lien
http://rruff.geo.arizona.edu/AMS/result.php
et taper ensuite "silicon" - ou le nom de toute autre substance solide: diamond, quartz, zircon, etc ...
Dernière modification par Wiwaxia (25-04-2022 17:20:53)
Hors ligne
#34 02-05-2022 20:53:30
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonsoir à tous !
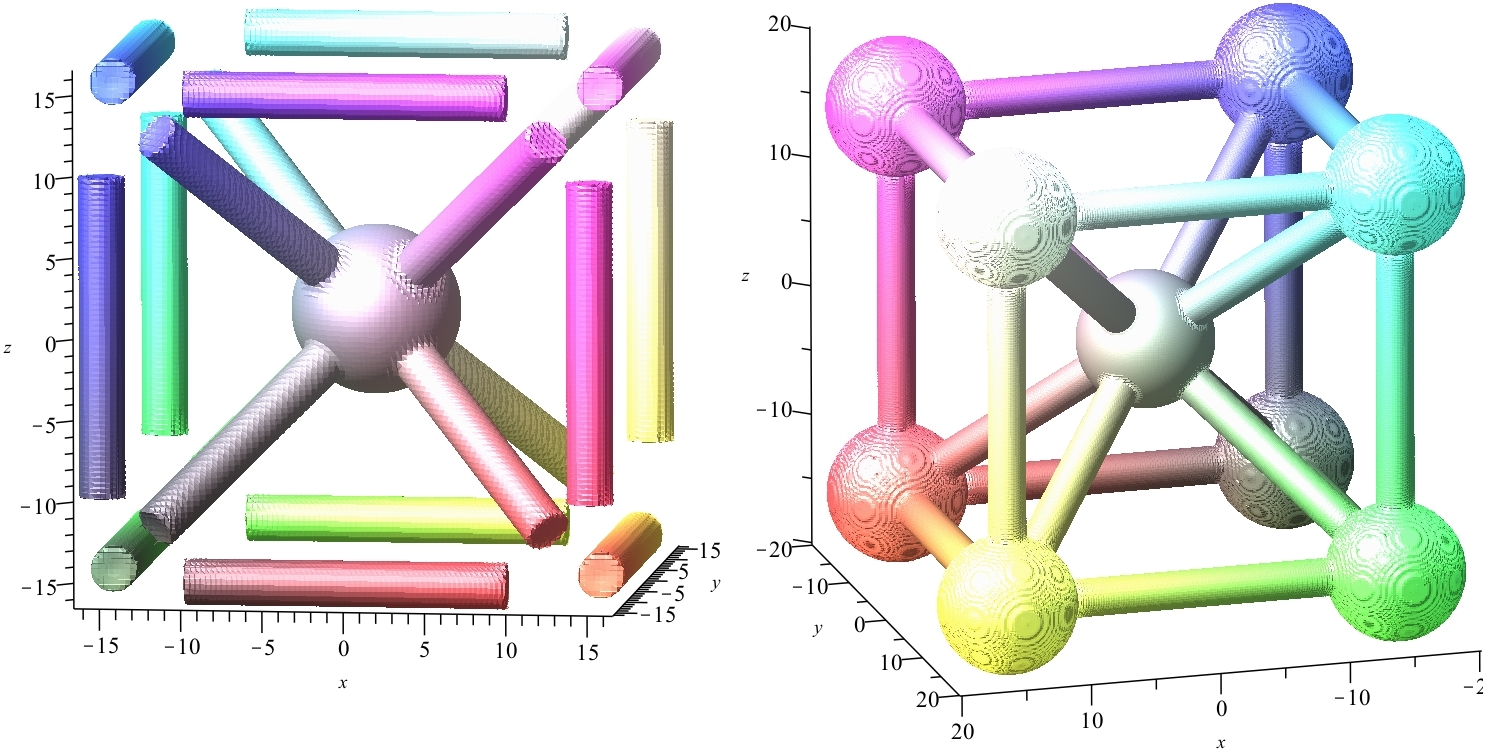
L'aventure de l'Atomium de Bruxelles se continue ici, quasi finie !
Vous voyez que ce qui manque est en bleu avec la sphère centrale. Nous allons construire ça, d'une certaine façon (opportuniste), car il y a sans doute d'autres façons de faire !
Nous allons fabriquer la partie centrale, c'est à dire la sphère centrale, de laquelle rayonnent 8 tubes (en bleu) rejoignant les 8 sphères aux sommets du cube. Vous voyez cela juste au-dessus de l'image noire, en #33 ! Après il restera à l'assembler avec la partie "cube", en faisant coïncider les 8 sphères ... avec quelques surprises !
La suite pour demain, bonne soirée !
Bernard-maths
Dernière modification par Bernard-maths (03-05-2022 10:11:11)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#35 03-05-2022 10:31:29
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour à tous !
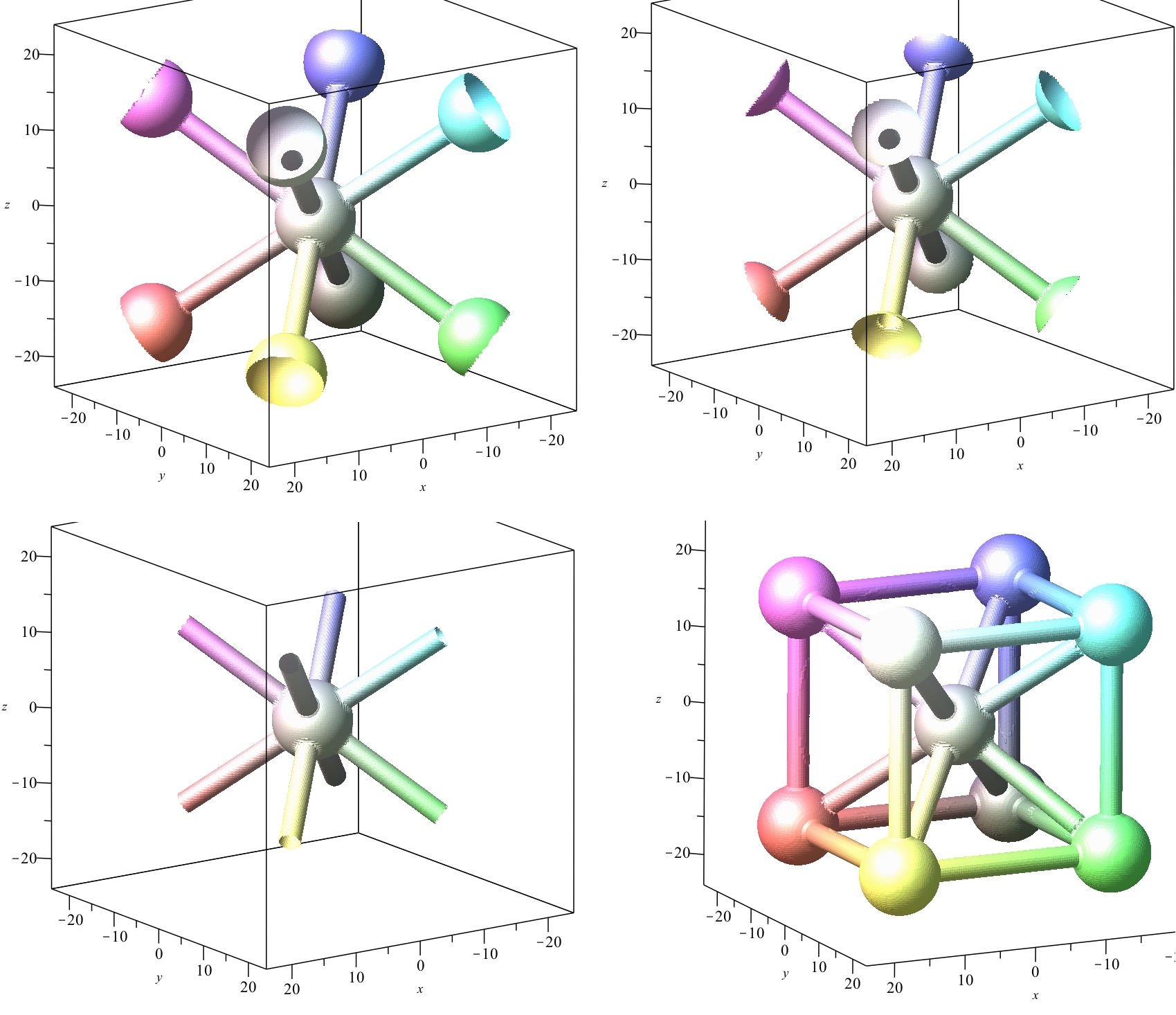
Voici en 5 étapes comment fabriquer "le centre" de l'atomium : en 5 équations Eq0 à Eq4, et en 5 figures correspondantes.
Je vais charger 2 images avec https://zupimages.net.
Soit des (vraies) images :
La 1ère est formée par 2 sphères en forme haltère, centrées en x = -15 et x = 15. Voir Eq0 plus bas. La 2ème est translatée vers la droite de 15, pour mettre la sphère de gauche centrée en O, voir Eq1. Ensuite on fait tourner cette haltère pour la mettre en position "grande diagonale" d'un cube ! Voir Eq2 et Eq3 plus bas. Sur Eq2 on tourne "vers le haut" autour de (y'y) d'un angle d'environ 35°et demi, dans le sens rétro, donc -35° ... Puis en Eq3, on tourne autour de (z'z) de 45° pile dans le sens trigo.
Enfin en Eq4, on utilise les 3 symétries plans du repère, les x, y et z devenant abs(x), abs(y) et abs(z). Et voilà la figue centrale de l'atomium terminée !
Et les programmes Maple associés :
Pour toute explication complémentaire, posez vos questions ...
Bernard-maths
Dernière modification par Bernard-maths (04-05-2022 16:52:34)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#36 04-05-2022 05:39:18
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour à tous !
Après la discussion #35 d'hier = ce matin, il reste à faire l'assemblage de ce "centre" avec le "tour", en quelques manipulations ...
Je vais charger des images avec https://zupimages.net.
Pour commencer les 2 morceaux à assembler, et à mettre à la même échelle !
En 1ère figure le cube de base extérieur, de profil, et de face en 2ème figure. On voit là que les sphères sont centrées sur des coordonnées en -15 ou +15.
Sur la 3ème, le centre de l'atomium tel que fabriqué en #35 est "trop grand", les sphères sont centrées en -** ou +**, avec ** > 15. Un coefficient k = Rac(3)/2 permet de réduire cette figure, on a alors la 4ème, sphères bien centrées en -15 ou +15.
Ci-dessous vous avez les équations Eq5 et Eq6 des 2 morceaux mis à la même échelle.
Puis les équations Eq7 et Eq8, Eq7 pour l'assemblage des 2 morceaux, en équation-produit. MAIS les 8 sphères ont disparu ! Voilà un "mystère" du tracé de Maple qui ne trace pas 2 fois la même sphère, mais en fait une sorte de "soustraction" !?
Avec Eq8, rebelote ! On met une 3ème couche de sphères ... c'est joli, non ?
Voilà, on va encore tourner autour pour trouver une "bonne équation globale", si elle existe ...
Pour toute explication complémentaire, posez vos questions ...
Bernard-maths
Dernière modification par Bernard-maths (04-05-2022 17:46:29)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#37 05-05-2022 10:15:01
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour à tous !
On a vu que la superposition de sphères les supprime ! Mais on avait déjà remarqué en #34 que ce qui manque au cube des 8 sphères, c'est la sphère centrale et les 8 tubes (en bleu #33) qui rejoignent les 8 sphères du cube. Donc on peut essayer de se limiter à ce genre de centre, en supprimant les 8 sphères du centre ...
Géométriquement un tel centre réduit se trouve à l'intérieur d'une sphère de centre O et de rayon rr limité à la longueur des tubes ... ce qui mène à rr = c0*sqrt(3) - r !
Voici des figures et des équations :
Les 2 1ères vous montrent la limitation du centre par une sphère. l'équation utilisée "ouvre" l'objet. La 3ème figure est le cas limite de rr pour arriver "ras" les sphères du cube. Puis vous avez l'assemblage. MAIS avec une formule légèrement différente : multiplication au lieu de division par la contrainte de la sphère limite ! Je cherche à arranger ça ... !???
En fait je pense depuis longtemps à un cube tronqué aux sommets, qui arrangerait bien les 2 morceaux à assembler, ou un truc s'approchant du rhombicuboctaèdre ... procrastination ...
Les 2 équations du centre raccourci, et de l'assemblage.
Bernard-maths.
Dernière modification par Bernard-maths (05-05-2022 11:55:41)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#38 25-03-2023 18:18:52
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour à tous !
Je suis à Castanet-Tolosan pour Maths en Scène !
En #31, je vous disais "à plus tard" !
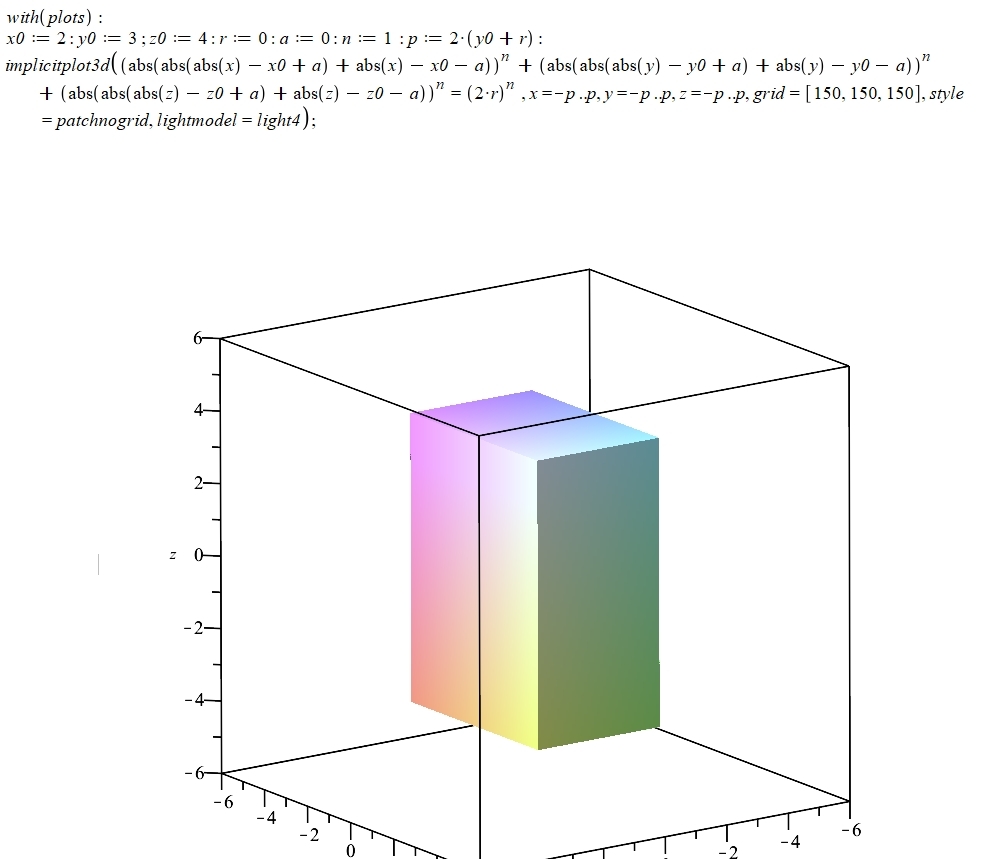
Voici une application de la formule multiple : le parallélépipède rectangle !
A vous de varier encore ...
Bernard-matths
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#39 30-03-2023 17:54:03
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonsoir Wiwaxia ! Bonsoir à tous !
Après étude de cette dernière équation, je crois qu'il y a un OS !!!
Je pense qu'on devrait obtenir un parallélépipède rectangle certes, mais PLEIN. Ce qui ne se verrait pas vraiment sur la figure ...
Mais en regardant l'intérieur, on voit qu'il est vide ! Problème de tracé avec Maple ???
Alors si quelques uns peuvent reprendre les calculs, et me confirmer ma remarque, MERCI !
Bernard-maths
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#40 30-03-2023 21:12:28
- Roro
- Membre expert
- Inscription : 07-10-2007
- Messages : 1 565
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonsoir,
Il est normal que ton parallélépipède ne soit pas plein puisqu'il est défini par une égalité de la forme $f(x,y,z)=0$.
Si tu veux un objet plein, il faut mieux utiliser des inégalités comme $f(x,y,z)<0$...
Roro.
Hors ligne
#41 30-03-2023 21:38:34
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonsoir Roro !
Désolé ! Une égalité peut très bien définir une zone pleine.
Par exemple, en général, si f(x,y) = 0 définit une courbe du plan, alors on sait que la courbe partage le plan en 3 zones : la courbe, le "côté" f(x,y) > 0 et le "côté" f(x,y) < 0. Ces 2 derniers sont des portions du plans ...
Qu'on peut définir par des égalités de la forme : f(x,y) + abs(f(x,y)) =0 et f(x,y) - abs(f(x,y)) =0 ...
Pour l'équation en question, elle se présente sous la forme : abs(f(x)) + abs(g(y)) + abs(h(z)) = 0.
Ce qui donne le système de 3 équations { f(x)=0 et g(y)=0 et h(z)=0 } ; ce qui me donne x dans [-x0, x0] et y dans [-y0, y0] et z dans [-z0, z0] ... donc un truc plein !
Bonne nuit ... nnnnnnn ...
Dernière modification par Bernard-maths (30-03-2023 21:39:41)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#42 31-03-2023 15:47:26
- Roro
- Membre expert
- Inscription : 07-10-2007
- Messages : 1 565
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour,
En effet Bernard, l'équation $x+|x|=0$ est vraie si et seulement si $x\ge 0$... tu as raison.
Par contre, cette équivalence me semble très "instable" numériquement.
Je m'expliques : si au lieu de résoudre $x+|x|=0$ tu résous, pour $\varepsilon>0$ fixé (petit !), l'équation $x_\varepsilon+|x_\varepsilon|=\varepsilon$ alors tu n'auras pas du tout l'inégalité $x_\varepsilon\ge 0$ mais plutôt l'égalité $x_{\varepsilon} = \frac{\varepsilon}{2}$.
Peut être qu'il faut regarder de ce coté ?
Roro.
Hors ligne
#43 31-03-2023 16:41:53
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour !
Merci pour tes essais. Mais je vais repousser la recherche de ce problème à plus tard ?
Cependant l'utilisation de ces formules sur GeoGebra et sur Maple a provoqué des instabilités et des perturbations dans les fichiers, j'en ai perdu un !!! C'est donc "un peu étrange" ... de plus la demande d'ouverture plante Maple !!!
Je vais reprendre la suite des variantes possibles, en choisissant quelques étapes dans ces variantes possibles !
Bernard-maths
Dernière modification par Bernard-maths (31-03-2023 17:24:11)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#44 11-04-2023 19:50:06
- Wiwaxia
- Membre
- Lieu : Paris 75013
- Inscription : 21-12-2017
- Messages : 411
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour,
J'avoue être complètement perdu dans l'imbrication des valeurs absolues ... et - plus grave à mon sens - ces complications paraissent inutiles, dans la mesure où l'expression
F(u, k) = |u + k| + |u - k] - 2k avec k > 0
conduit facilement à l'équation d'un prisme droit à base rectangulaire, puisqu'elle prend les valeurs:
# pour u < -k : F(u, k) = -2(u + k) > 0 ;
# sur [-k ; +k] : F(u, k) = 0 ;
# pour u > k : F(u, k) = 2(u - k) > 0 ;
le prisme droit à base rectangulaire centré à l'origine du repère, de demi-arêtes (a, b, c) et dont les faces sont normales aux axes admet ainsi pour équation:
G(x, y, z) = F(x, a) + F(y, b) + F(z, c) = 0 .
Cette équation caractérise non pas la surface délimitante de l'objet, mais le domine tout entier:
|x| ≤ a ; |y| ≤ b ; |z| ≤ c .
La discontinuité que présente le vecteur Grad(G) sur la frontière est probablement à l'origine des perturbations obsevées dans l'exécution du programme; cela dépend de ce que fait l'algorithme.
Hors ligne
#45 11-04-2023 20:47:48
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonsoir Wiwaxia !
Les perturbations ont disparu après avoir redémarré ... ???
Mais les tracés sur Maple restent en surface, et non en volume.
Poutant j'ai déjà fait des tracés en volume, ça se voit !
J'ai eu beaucoup de préoccupations depuis le début du mois, je reprendrai plus tard ...
Bonne soirée, Bernard-maths
Dernière modification par Bernard-maths (11-04-2023 20:48:38)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne
#46 12-04-2023 11:01:14
- Bernard-maths
- Membre
- Lieu : 34790 Grabels
- Inscription : 18-12-2020
- Messages : 1 337
Re : Les figures rayonnantes : principes, équations, et jolis dessins !
Bonjour !
L'imbrication des valeurs absolues tient au fait que je pars d'une équation plus complexe !
Et je cherche les différents cas qui peuvent se présenter ... selon des situations diverses ...
Il y a au moins 6 paramètres, et même 8 ou 9 ?, ce qui donne beaucoup de cas particuliers !!!
On a 2 équations qui doivent donner un prisme plein, MAIS qui ne s'écrivent pas pareillement : donc, comme tu dis, cela doit dépendre de l'interprétation qu'en fait l'algorithme de Maple ...
Il faut que je m'assure de cette divergence, et alors d'en parler à Maple !?
@ +, B-m
PS : un ex de polyèdre plein :
https://www.bibmath.net/forums/viewtopi … 450#p94450
Dernière modification par Bernard-maths (12-04-2023 11:47:02)
Ma philosophie est immuable : l'immobilisme tue ...
Les Anciens ont trouvé le plus facile ... il nous reste le plus dur !
Hors ligne