Forum de mathématiques - Bibm@th.net
Vous n'êtes pas identifié(e).
- Contributions : Récentes | Sans réponse
- Accueil
- » Le coin des beaux problèmes de Géométrie
- » Plus grand périmètre
- » Répondre
Répondre
Résumé de la discussion (messages les plus récents en premier)
- FFR
- 27-08-2022 15:08:29
Bonjour,
Bien que résolu par Mathafou je me permets de rouvrir ce problème de l’année dernière, car il me semblait intéressant de poursuivre la voie de Wiwaxia surtout que 99% du travail avait été fait.
Il était arrivé à la conclusion :
$\frac{\sin \alpha }{R_1 \times a}= \frac{\sin \beta }{R_2 \times b}= \frac{\sin \gamma }{R_3 \times c}= K$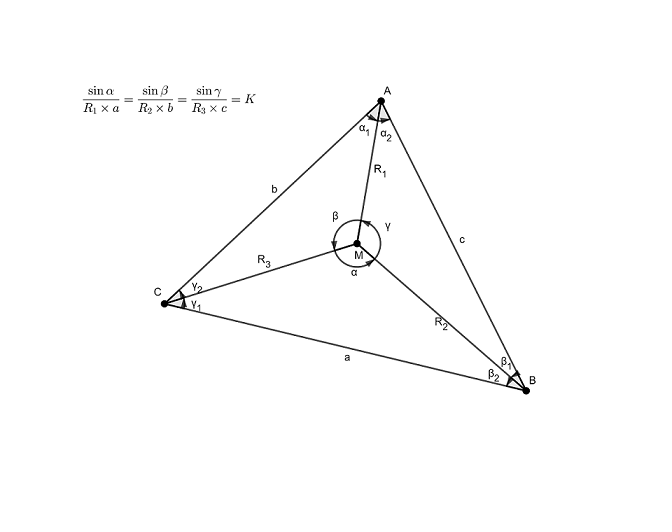
La loi des sinus dans un triangle, appliquée respectivement aux triangles AMB, BMC et CMA permet d’établir les égalités suivantes :
$\frac{R_2}{\sin \alpha_2}= \frac{R_1}{\sin \beta_1}= \frac{c}{\sin \gamma }= \frac{1}{K \times R_3}$
$\frac{R_3}{\sin \beta_2}= \frac{R_2}{\sin \gamma_1}= \frac{a}{\sin \alpha }= \frac{1}{K \times R_1}$
$\frac{R_1}{\sin \gamma_2}= \frac{R_3}{\sin \alpha_1}= \frac{b}{\sin \beta }= \frac{1}{K \times R_2}$
D’où :
$\sin \alpha_1= \sin \alpha_2= K \times R_2 \times R_3$
$\sin \beta_1= \sin \beta_2= K \times R_3 \times R_1$
$\sin \gamma_1= \sin \gamma_2= K \times R_1 \times R_2$
Comme le triangle n’est pas plat,
$\alpha_1= \alpha_2$
$\beta_1= \beta_2$
$\gamma_1= \gamma_2$
François.
- Wiwaxia
- 10-07-2021 18:15:36
Bonjour,
J'ai complété le programme précédent par le calcul dans le repère (Mxy)
# des vecteurs unitaires (Uma, Umb, Umc) associés aux positions respectives des 3 points (A, B, C) - ce dernier étant placé sur la partie positive de l'axe (x'x), et (B) présentant une ordonnée positive,
# et de ceux (Wabc, Wbca, Wcab) associés aux bissectrices des angles (AB, AC), (BC, BA),(CA, CB);
d'après ce qui a été établi, ils sont théoriquement opposés, et leur déterminant nul.
Les valeurs obtenues pour ce dernier, au plus égales à environ 10-18 en valeur absolue, restent compatibles avec la précision limite assurée par le logiciel (10-19), compte tenu du cumul des erreurs d'arrondi accompagnant les calculs.
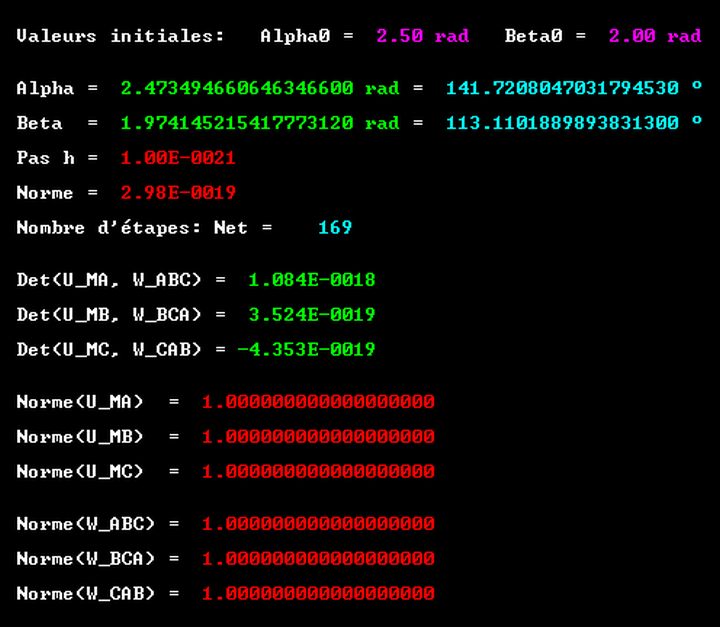
Les valeurs des normes ont été affichées à des fins de vérification.
- Bernard-maths
- 08-07-2021 05:39:26
Bonjour Wiwaxia !
Mon idée est de prendre les choses à l'envers ! On se place donc dans la situation où les bissectrices se coupent en M.
SI la conjecture est bonne, on doit pouvoir prouver qu'en déplaçant un des 3 points, alors le périmètre diminue ... ?
Pour cela, je considère 3 cercles concentriques (donc quelconques ?), et je place le point A sur un cercle (donc C1).
Puisque [AM] est la bissectrice de l'angle (BAC), alors les côtés [AB) et [AC) sont symétrique par rapport à [AM) ...
Donc, si je place B sur un cercle (C2), C sera sur le 3ème cercle, à l'intersection avec le symétrique de [AB) ...
On peut donc déterminer les coordonnées de C à partir de celles de B ...
Alors si x = xB est "la variable choisie", pour "avoir C", on doit passer par une équation (compliquée) du 4ème degré, avec des racines peut-être ... enfin pas triste ... donc pouvoir calculer le périmètre, et s'amuser à en chercher le maximum ... et voir que finalement ce sera quand [BM) et [CM) sont les bissectrices ...
Si on fixe A sur (x'O[, alors xA = - rayon de C1, alors x = xB variera entre ? et ? sur un intervalle parcouru une seule fois ... à adapter ...
Voilà mon idée, en gros, mais je suis très pris avec ma nouvelle discussion avec MAX !!!
Cordialement, Bernard-maths
- Wiwaxia
- 07-07-2021 08:02:40
Bonjour Bernard-maths,
... Si on prend A fixé, B variable sur le cercle (concerné), et C sur le 3ème cercle et côté adéquat de l'angle en A, en choisissant x = xB comme variable, on peut exprimer périmètre = f(xB), et donc trouver xB, montrer que les 3 bissectrices sont bien comme on veut ... etc ...
Ton hypothèse suppose la donnée arbitraire des 3 cercles concentriques, donc celle de leurs rayons respectifs (R1, R2, R3); on ne peut alors choisir, dans le cas particulier du périmètre maximal, que la position de l'un des 3 points (A, B, C); celles des deux autres s'en déduisent par les valeurs des angles (α) et (β), qui dépendent des rapports (R3/R1) et (R3/R2).
Cordialement, W.
- Bernard-maths
- 06-07-2021 21:48:23
Bonsoir à tous !
... le problème me semblait résolu avec la symétrie bissectrice ... mais je ne l'ai pas fait ... donc ?
Si on prend A fixé, B variable sur le cercle (concerné), et C sur le 3ème cercle et côté adéquat de l'angle en A, en choisissant x = xB comme variable, on peut exprimer périmètre = f(xB), et donc trouver xB, montrer que les 3 bissectrices sont bien comme on veut ... etc ...
Puis enfin montrer que si on n'est pas en situation bissectrices, alors périmètre n'est pas maximal !? Non ?
Voilà, ça me paraît une voie à suivre, mais j'ai pas le temps !!! ...
Bonne soirée, bernard-maths
- Wiwaxia
- 06-07-2021 14:46:48
Bonjour,
Voici le problème :
Soit un M du plan et 3 cercles C1,C2 et C3, distincts, de centre M et de rayon respectifs R1,R2 et R3.
Trouver 3 points A,B et C respectivement sur C1, C2 et C3 de façon que le triangle ABC ait un périmètre maximal.
Les valeurs des rayons étant données, ainsi que les positions du centre commun (M) et de l'un des trois points (A, B, C), il est possible de déterminer celles des deux autres par l'exploration des valeurs de la fonction F(α, β) = [Ua2 + Ub2]1/2, et la recherche du zéro non-trivial sur le domaine [0, π]2.
La comparaison systématique de la valeur actuelle de la fonction F(α, β)
à celles observées aux quatre points voisins, de coordonnées (α ± h, β) , (α, β ± h),
permet de localiser l'extremum dans des limites de plus en plus étroites, compatibles avec la précision des calculs effectués par le logiciel (Virtual Pascal, en l'occurrence). Le pas (h), initialement égal à (0.1), est divisé par (10) lorsque la plus faible valeur calculée correspond au point central.
Les mêmes valeurs des rayons (Rj = 1, 2, 3) conduisent aux résultats suivants:
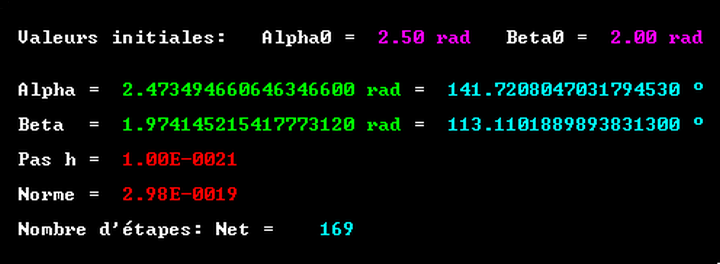
La comparaison avec ceux découlant de la division de l'image en pixels (déjà partiellement publiés)
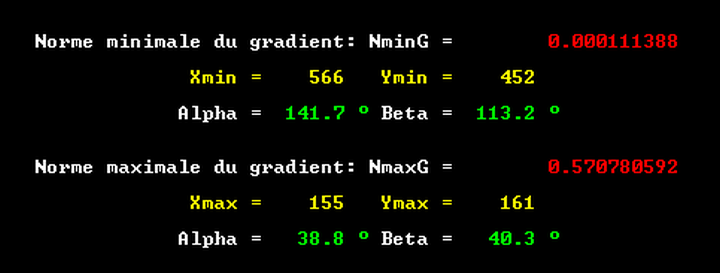
permet les constats suivants:
a) les limites obtenues pour les coordonnées (α, β) sont effectivement très proches des valeurs approchées citées auparavant - l'écart ne dépassant pas 0.1 ° ;
b) la valeur minimale obtenue (~ 3.0E-19) apparaît très inférieure au maximum repéré sur le domaine (~ 0.57), et peut être considérée comme nulle; en effet le rapport Fmin/Fmax = 5.3E-19 ,
quoique nettement supérieur au "epsilon machine" lié à la codification des nombres à virgule flottante (ici 2-63 = 1.1E-19) - s'explique aisément par la dérive due à la lourdeur des calculs.
Le procédé définit une suite double convergeant vers une limite unique sur un domaine relativement large - en fait tant que le point initial ne s'approche pas trop des frontières de la cuvette dont on recherche le point le plus bas:
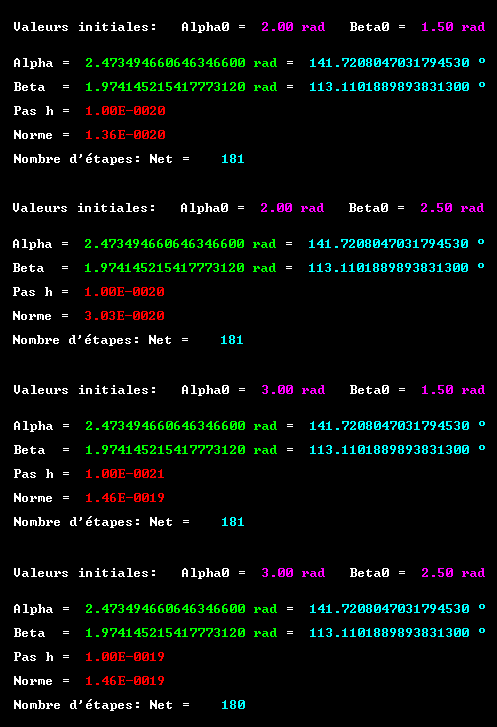
Les coordonnées limites apparaissent indépendantes de leurs valeurs initiales; le calcul du minimum local conduit à des valeurs très faibles (Fmin/Fmax >~ 2.4E-20) et très dispersées: il s'agit en fait d'un minimum nul.
- mathafou
- 23-06-2021 16:58:35
Rebonjour,
et pour appliquer ça au problème initial :
et le fichier Geogebra : Geogebra
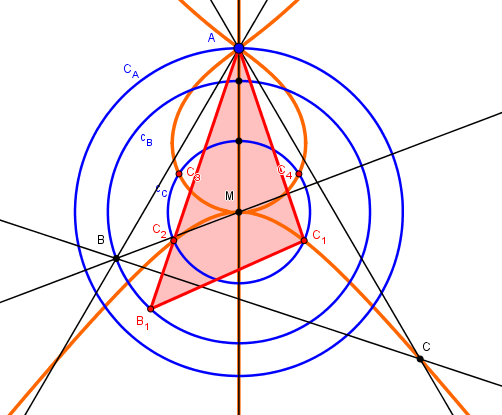
principe : on se fixe A
B variable sur sur son cercle et on construit C dans le plan avec M intersection des bissectrices (simples symétries)
Le lieu de C quand B varie est tracé et ses intersections avec le cercle Cc donnent les solutions
incluant les "solutions", "périmètre minimum" et "triangles dégénérés aplatis sur (AM) (on fait le tri à la main)
- mathafou
- 23-06-2021 15:47:02
Bonjour,
lemme
étant donnée une courbe [tex]\Gamma[/tex] (quelconque) et deux points A et B, le point C de [tex]\Gamma[/tex] avec CA+CB maximum (resp. minimum) est tel que la normale en C à [tex]\Gamma[/tex] soit bissectrice de [tex]\angle ACB[/tex]
en effet les courbes de niveau des points C avec CA+CB = constante sont des ellipses de foyers A et B
CA+CB sera maximum (resp. minimum) si [tex]\Gamma[/tex] est (localement) intérieure (resp. extérieurre) à cette ellipse
et donc si l'ellipse est tangente en C à [tex]\Gamma[/tex]
comme C est sur une ellipse de foyer A et B la normale commune aux deux courbes (perpendiculaire à la tangente commune) est bissectrice des rayons vecteurs CA et CB
si [tex]\Gamma[/tex] est un cercle de centre M, la normale passe par M. CQFD
- Bernard-maths
- 20-06-2021 17:51:18
Bonsoir à tous !
Je viens de rectifier une erreur "de frappe", car je sais bien que (AB) et (AC) ne sont pas parallèles !!!
Il faut refaire la figure, en fixant A comme il est, en plaçant B sur c2, en traçant la symétrique de (AB) passant par A, prendre C = intersection de c3 et cette symétrique ... et voir ce qu'il se passe ...
Vous pouvez y aller !
Bernard-maths
- Wiwaxia
- 20-06-2021 17:16:48
Par curiosité, j'ai regardé ce que l'on pouvait obtenir dans le cas R1 = 1 , R2 = 2 , R3 = 3
par un graphe faisant apparaître les valeurs extrêmes de la norme du vecteur Grad(p) - plus précisément de son expression simplifiée.
Ce qui est en cause, c'est la présence d'un minimum nul hors des sommets du domaine; les valeurs données pour les angles sont bien sûr approchées; elles résultent d'un calcul rapide, lié à la résolution de l'image en un nombre fini de pixels.
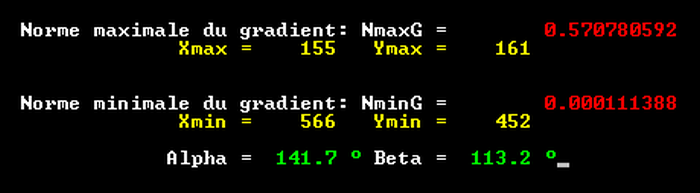
La connaissance du maximum est indispensable à la détermination d'une échelle appropriée.
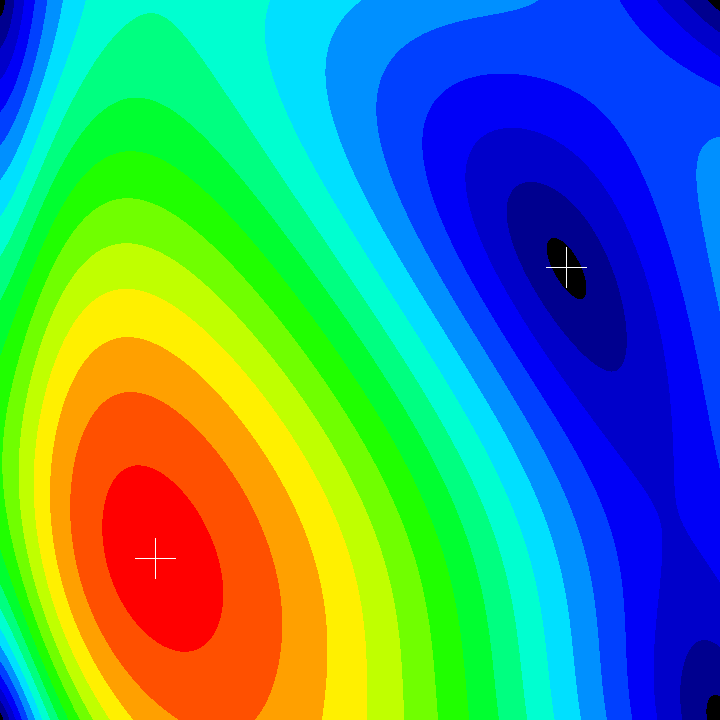
- Wiwaxia
- 20-06-2021 17:04:01
Bonjour,
... Je constate, mais ne vois pas encore quoi faire ...
... / ...
Sur cette figure (AB) // (AC). Peut-on montrer que si on prend B' différent de B, alors le périmètre de AB'C diminue ?
Il suffit de s'assurer que les relations caractérisant l'extremum du périmètre sont bien vérifiées.
On peut d'ailleurs envisager une exploration systématique des éventuelles solutions (α, β) sur un domaine bidimensionnel [0 ; π]x[0 ; π], pour des valeurs arbitraires des 3 rayons.

PS: Des erreurs ont été corrigées, qui n'affectaient pas le tracé du graphique.
- Duareb1
- 18-06-2021 11:47:50
Bonjour,
Géogebra (encore lui...) m'a conduit à une autre conjecture qui, si elle était démontrée, deviendrait un lemme utile pour la suite. Voici le problème annexe :
Soit un cercle de centre M et deux points A et B situés à l'extérieur du cercle. Soit C un point du cercle. Trouver la position de C pour que CA+CB soit maximale.
Et la conjecture : CA+CB est maximale si (CM) est la bissectrice de l'angle ACB.
- Bernard-maths
- 18-06-2021 11:02:56
Bonjour à tous !
Je constate, mais ne vois pas encore quoi faire ...
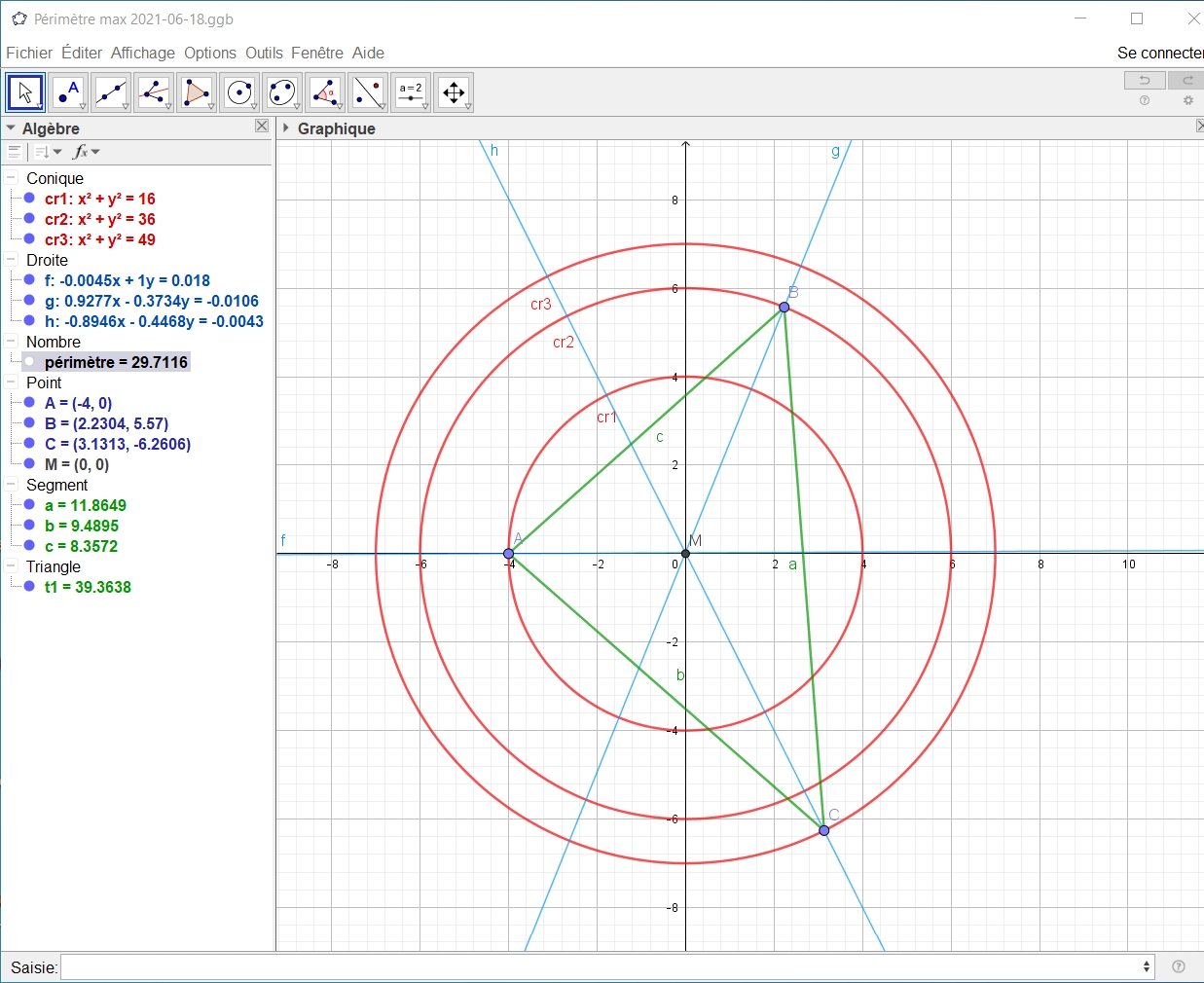
Sur cette figure (AB) // (AC) !!! Non, (AB) et (AC) symétriques par rapport à la bissectrice = axe des x !!! (Rectifié le 20-06-2021 ...). Peut-on montrer que si on prend B' différent de B, alors le périmètre de AB'C diminue ?
Bernard-maths
- Wiwaxia
- 18-06-2021 10:05:25
Bonjour,
Il y a bien une solution analytique au problème, mais son exploitation est assez difficile, et je ne vois pas comment faire apparaître la propriété géométrique évoquée ...
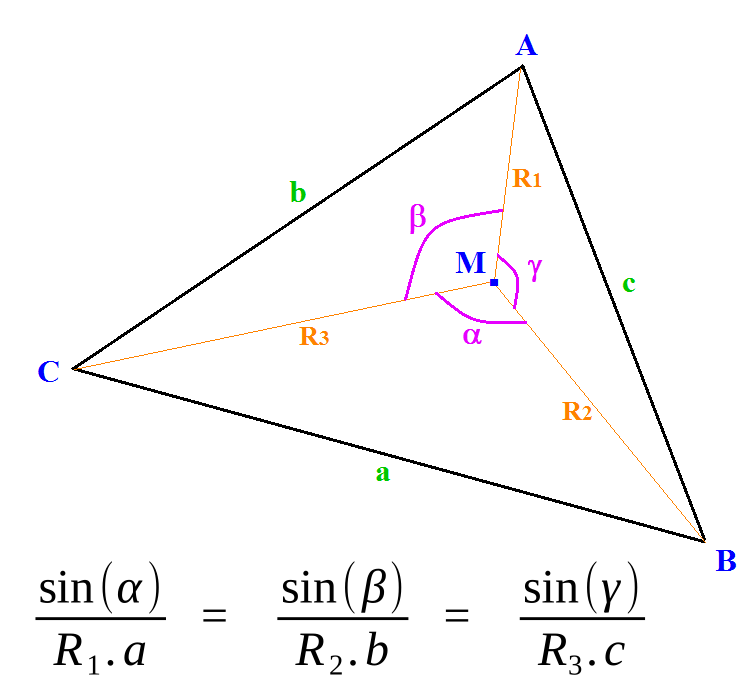
- Duareb
- 16-06-2021 22:17:08
Bonjour,
Voici le problème :
Soit un M du plan et 3 cercles C1,C2 et C3, distincts, de centre M et de rayon respectifs R1,R2 et R3.
Trouver 3 points A,B et C respectivement sur C1, C2 et C3 de façon que le triangle ABC ait un périmètre maximal.
Le logiciel Geogebra m'a conduit à énoncer une conjecture : Quand ABC est construit alors M est le point de concours des bissectrices intérieures du triangle ABC.
Remarque : MA+MB+MC=R1+R2+R3= constante.
Je qualifie ce problème de "beau" dans la mesure où l'énoncé est simple à comprendre tout en cachant une réelle difficulté.
Je remercie d'avance ceux qui pourront m'apporter quelques éléments de démonstration.








