Forum de mathématiques - Bibm@th.net

Math17

Invité

calculer le point d'intersection entre une courbe Bézier et une droite

Bonjour,

Je crois que tout est dans le titre;
Je connais les points P0, P1, P2, P3, D1 et D2 qui forment une courbe de Bézier cubique et une droite.
Mon but est de calculer les coordonnées de I, le point d’intersection entre la droite et la courbe.

Ca a l'air simple comme ça mais je suis nul en math et je ne sais pas comment faire.
Voici un shéma.

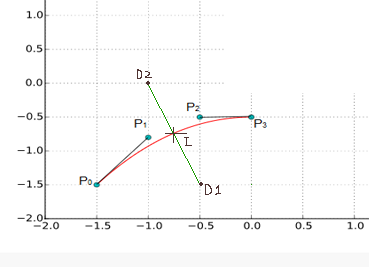
Pouvez vous m'aider sur la façon de procéder ?

Merci d'avance !

Zebulor

Membre expert

Inscription : 21-10-2018

Messages : 2 090

Re : calculer le point d'intersection entre une courbe Bézier et une droite

Bonsoir,
Nul en maths ? tss tss ça n'existe pas des êtres humains nuls en maths !
les points M(x,y) de la courbe rouge (dont le point I) appartiennent à une courbe vérifiant l'équation paramétrique en $t$ qu'on a du te donner...et si tu ne l’as pas, je l’ai trouvée..car je decouvre les courbes de Bézier...
Quand t=0, M est en $P_0$ et quand t=1 il est en $P_3$. Entre ces deux valeurs extrêmes M se trouve en I, à $t=t_I$. Pour trouver les coordonnées de I, il faut donc trouver $t_I$.

On a pour l'instant 3 inconnues et 2 équations indépendantes, que sont les projections de l'équation paramétrique ci dessus sur les axes Ox et Oy.
Il manque donc une troisième équation : celle reliant $x_I$ et $y_I$, qu'on peut trouver sachant que I est sur la droite $(D1D2)$

3 équations indépendantes, 3 inconnues $x_I$, $y_I$ et $t_I$. Reste à résoudre le système, équivalent à une équation à une inconnue $t_I$, que tu réinjectes dans l'équation paramétrique pour obtenir les coordonnées de I.

Dernière modification par Zebulor (27-11-2019 22:07:47)

---

En matière d'intégrales impropres les intégrales les plus sales sont les plus instructives.

Math17

Invité

Re : calculer le point d'intersection entre une courbe Bézier et une droite

Merci pour ta réponse, Zebulor.

Ok alors je crois avoir compris globlement ce que tu dis...cependant je ne vois pas comment on peut trouver tI alors qu'il n'est qu'un paramètre ?

Pour l'équation qui construit la courbe bézier cubique je me suis basé sur l'équation de f.egrand :

P(t)=(1-t)3P0+3t(1-t)2P1+3t2(1-t)P2+t3P3,

t étant effectivement un paramètre allant de 0 à 1.

Zebulor

Membre expert

Inscription : 21-10-2018

Messages : 2 090

Re : calculer le point d'intersection entre une courbe Bézier et une droite

Re,
$t$ n’est qu un paramètre mais en observant bien la courbe rouge :
En $t=0$, le point que j.appelle $M(x(t);y(t))$ est en  $P_0$ et lorsque $t$ croît, $x$ croît strictement et il en est de même pour $y$, jusqu’à ce que M se trouve en $P_3$ pour $t=1$.
Cela peut se montrer par le calcul depuis l'équation de Legrand en cherchant $x'(t)$ et $y'(t)$. Au passage ce lien utile et éclaircissant, je n'ai pas trouvé mieux ailleurs :
http://www.bibmath.net/ressources/index … ezier.html
avec cette équation : $\overrightarrow{OM(t)}=(1-t)^3\overrightarrow{OP_0}+3t(1-t)^2\overrightarrow{OP_1}+3t^2(1-t)\overrightarrow{OP_2}+t^3\overrightarrow{OP_3}$ où O est un point quelconque qu'on peut donc prendre en $P_0$ pour simplifier encore cette dernière équation et réduire le nombre de futurs calculs.

A chaque valeur de $t$ correspond donc une seule valeur de $x$ et une seule valeur de $y$.
La relation entre $x$ et $t$ est  fonctionnelle et c'est même une bijection d'après la phrase précédente : je l'appelle $f$.
De même pour la relation entre $y$ et $t$ : je l’appelle $g$.

L’équation de la fin de ton dernier post une fois projetée sur les axes Ox et Oy donne donc 2 équations
1) $x=f(t)$
2) $y=g(t)$
où $f$et $g$ sont à priori différentes ici car les points de la courbe rouge ne décrivent pas la droite d équation $y=x$.

Il se trouve que le point I appartient :
- à la courbe rouge donc il lui correspond une valeur de t unique : $t_I$. D.où $x_I$=$f(t_I)$ et  $y_I$=$g(t_I)$
- à la droite D1D2, ce qui donne une relation entre les coordonnées de I, d où l’existence d une troisième fonction h, celle ci est affine , telle que $y_I=h(x_I)$ où $h$ est aussi une bijection.

Cette dernière équation est équivalente par subsitution à  : $g(t_I)=h(f(t_I))$ : équation E
Une équation à une inconnue $t_I$ où $t_I$ est unique sur [0;1] : E le confirme car $g$ est une composée de bijections sur [0;1]. Lorsque t passe de 0 a 1 le point M ne passe bien qu’une seule fois en I.
$t_I$ est une valeur qu’on reporte ensuite dans 1) et 2) pour obtenir $x_I$ et $y_I$...

Voilà pour le principe, la suite est purement calculatoire. Il y a peut être une méthode plus simple mais pour le moment je n’en vois pas..tu as raison : la simplicité est apparente ..mais c'est faisable!

Dernière modification par Zebulor (02-12-2019 20:15:55)

---

En matière d'intégrales impropres les intégrales les plus sales sont les plus instructives.