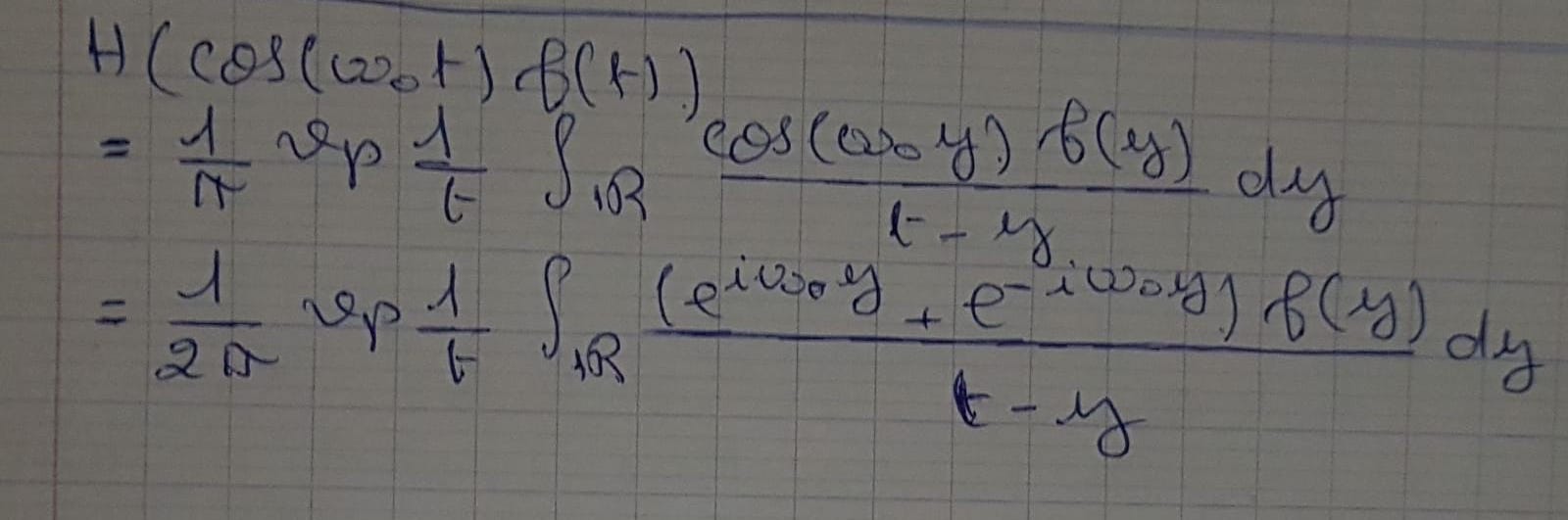Forum de mathématiques - Bibm@th.net

Sinoxis

Invité

Distributions et théorie de l’échantillonnage

Bonjour, j'essaye de résoudre cet exercice mais je ne vois pas comment on peux commencer dans la question 1, quelqu'un a une idée s'il vous plait ?

Roro

Membre expert

Inscription : 07-10-2007

Messages : 1 565

Re : Distributions et théorie de l’échantillonnage

Bonjour,

As-tu essayer de calculer $\mathcal F(H(f))$ ?

Utilise ensuite le fait que la transformation de Fourier est une isométrie sur $L^2$.

Roro.

Sinoxis

Invité

Re : Distributions et théorie de l’échantillonnage

Bonjour,

En calculant $\mathcal{F}(H(f))$ on trouve que : $\mathcal{F}(\frac{1}{\pi} \operatorname{vp} \frac{1}{x} * f)$ = $\mathcal{F}(\operatorname{vp}(1 / x)) \mathcal{F}(f)$ = $-i \pi \operatorname{sign}\mathcal{F}(f)$
est ce que cela suffit de dire que H peut se prolonger en une application continuité de $L^{2}(\mathbb{R})$ dans lui-meme en raison de le densité de $\mathcal{S}(\mathbf{R})$ dans $L^{2}$ ou il faut aussi montrer que $H$ est continue de $\mathcal{S}(\mathbb{R})$ dans $L^{2}(\mathbb{R})$ avec les normes $L^{2}$ des deux côtés ?

Roro

Membre expert

Inscription : 07-10-2007

Messages : 1 565

Re : Distributions et théorie de l’échantillonnage

Bonsoir,

Il suffit de montrer que tu as :
$\exists C \in \mathbb R \quad ; \quad \forall f \in L^2 \quad \|\mathcal F(H(f))\|_{L^2} \leq C \|\mathcal F (f)\|_{L^2}$
puisque par isométrie de $\mathcal F$ tu auras
$\exists C \in \mathbb R \quad ; \quad \forall f \in L^2 \quad \|H(f)\|_{L^2} \leq C \|f\|_{L^2}$

Par densité tu prolonges ta fonction $H$ à $L^2$, et le résultat ci-dessus te dit que cette application linéaire $H:L^2\to L^2$ est continue.

Roro.

Dernière modification par Roro (23-04-2020 22:00:44)

sinoxis

Membre

Inscription : 23-04-2020

Messages : 3

Re : Distributions et théorie de l’échantillonnage

Voici ma réponse , est ce que cela vous semble juste ?

Soit $f \in \mathcal{S}(\mathbb{R}),$ or $\mathcal{F}(H f)=$ $\frac{1}{\pi} \mathcal{F}(\operatorname{vp}(1 / x)) \mathcal{F}(f)=-i \operatorname{signe} \mathcal{F}(f) . \quad$Par conséquent, $\mathcal{F}(H f)$ est dans $L^{2}(\mathbb{R})$ et
$\|\mathcal{F}(H f)\|_{2}=\|\mathcal{F}(f)\|_{2}$ Comme $\mathcal{F}$ est une isométrie sur $L^{2}(\mathbb{R}),$ il s'ensuit que $H f \in$ $L^{2}(\mathbb{R})$ et que $\|H f\|_{2}=\|f\|_{2} .$ L'espace $\mathcal{S}$ étant dense dans $L^{2}(\mathbb{R}),$ l'application linéare $H$ s'étend en une isométrie de $L^{2}(\mathbb{R}) .$

Par contre dans la question 2 j'arrive pas à trouver l'expression , est ce que vous l'avez calculé ?

Roro

Membre expert

Inscription : 07-10-2007

Messages : 1 565

Re : Distributions et théorie de l’échantillonnage

Bonjour,

Ca me semble correct.
Je n'ai pas fait le calcul pour la question 2. Si on utilise le passage en Fourier et Fourier inverse, ça doit se faire...

Roro.

sinoxis

Membre

Inscription : 23-04-2020

Messages : 3

Re : Distributions et théorie de l’échantillonnage

Déjà est ce que vous etes d'accord avec ses deux lignes , si oui , comment on fait apparaitre la transformation de fourier ?

Dernière modification par sinoxis (24-04-2020 14:38:51)

sinoxis

Membre

Inscription : 23-04-2020

Messages : 3

Re : Distributions et théorie de l’échantillonnage

Comment on fait apparaitre la transformation de Fourier ?