Révision polynômes

yannD · 05-01-2020 12:47:33

Bonjour, voici un autre exercice pour préparer mon DS

ABCD est un carré de côté a. On place un point I sur le côté [AB], la parallèle à (AC)
passant par I coupe [BC] en J et la parallèle à (BD) passant par I coupe [AD] en L.
On complète le rectangle I J K L.
a) Faire une figure.
b) On pose $AI = x$. Exprimer à l'aide de $x$ les longueurs IJ et IL
c) Justifier que l'aire du rectangle IJKL vaut $2x(a - x)$.
d) Est-il possible que l'aire de IJKL soit la moitié de celle de ABCD ? Pour quelle position de I.
e) On prend a = 6. Où faut-il placer I pour que l'aire de IJKL soit u n t i e r s d e c e l le de ABCD ?

calcul la longueur IJ et de la longueur IL
nature du triangle ABC, on sait que son angle droit
de plus, les côtés [AB] et [BC] ont même longueur
on en conclut que le triangle ABC est un triangle rectangle isocèle
Puisque la droite (IJ) est parallèle à la diagonale [AC] de ce carré
alors BIJ est un triangle rectangle isocèle
On montrerait de même que le triangle AIL est aussi un triangle rectangle isocèle

Puisque le triangle BIJ est un triangle rectangle isocèle, on sait que son angle B est un angle droit
D'après le théorème de Pythagore IJ(au carré) = BI(au carré)+BJ(au carré)
soit IJ (au carré) = (a-x)au carré + (a-x)au carré
IJ(au carré) =
et puis, en terminant mes calculs, je n'arrive pas à trouver 2x(a-x) pour l'aire du rectangle, pouvez-vous m'aidez s'il vous plaît ?
yann

yoshi · 05-01-2020 15:51:45

Bonjour,

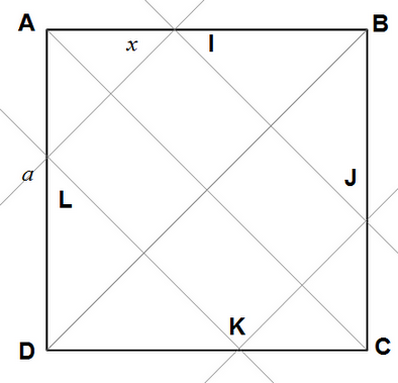
Pourquoi n'utilises-tu pas le Théorème de Thalès ;
- dans le triangle ABC sachant que $I \in [AB]$, $J \in [BC]$ et $(IJ) // (AC)$ pour calculer IJ ?
- dans le triangle ABD sachant que $I \in [AB]$, $L \in [AD]$ et $(IL) // (BD)$ pour calculer IL ?

Tes calculs en seraient grandement facilités !

Au passage, calcul de IJ pas terminé mais IJ² est juste...
Tu peux aussi procéder de la même façon pour IL si tu n'aimes pas Thalès...

Il doit y avoir erreur de calcul si tu ne tombes pas sur la bonne aire.
Montre-les nous !

@+

yannD · 05-01-2020 16:04:38

Bonjour Yoshi, merci de m'avoir répondu
Dois-je faire une démonstration pour dire que AI=AJ ?

yannD · 05-01-2020 16:05:58

j'ai pas vu que tu a s modifié
je vais mettre les calculs que j'ai fait

yannD · 05-01-2020 16:11:46

avant tout je veux faire la démonstration, parce que j'ai besoin de dire que le triangle est rectangle pour pouvoir utiliser le th de Pythagore
et il faut aussi que je dise qu'il est isocèle pour dire que AI = AL
il faut que je le fasse en deux temps :

Dans le triangle ABC, on sait que son angle est droit
de plus , ABCD est un carré donc AB = AC
Puisque (BD)//(IL) alors on peut dire que le triangle AIL est aussi un triangle rectangle isocèle.

et pour le calcul de IL
le triangle AIL est rectangle isocèle, d'après le th de Pythagore, on a :
$IL^2 = AL^2+AI^2$
$IL^2=x^2+x^2$
$Il^2=2x^2$
$IL=\sqrt{2x^2}$
$IL=2x$

$IJ^2=BI^2+BJ^2$
$IJ^2=(a-x)^2+(a-x)^2$
et là, je ne sais plus si je dois dire : $IJ^2=2(a-x)^2$
ou si c'est $IJ=\sqrt{(a-x)^2}+\sqrt{(a-x)^2}$

Dernière modification par yannD (05-01-2020 16:27:33)

yoshi · 05-01-2020 19:50:25

Re,

Désolé, la 1ere ligne est juste, la deuxième fausse :

$IL=\sqrt{2x^2}$
$IL=2x$

Rappel : $\sqrt{ab}=\sqrt a \times \sqrt b$
Donc $\sqrt{2x^2}=\sqrt 2 \times \sqrt{x^2}=x\sqrt 2$
Quant à IJ, je ne vois pas le résultat.
Avec ta méthode, $IJ^2=(a-x)^2+(a-x)^2=2(a-x)^2$
D'où IJ = ?...

Moi je te proposais plus simple, moins source d'erreurs, mais tu fais bien comme tu veux...
Je me fiche de savoir que BIJ est isocèle ou qu'il est rectangle.
Je considère le triangle ABC, je sais que (IJ)//((AC), je peux donc écrire que :
$\dfrac{BI}{BA}=\dfrac{BJ}{BC}=\dfrac{IJ}{AC}$
Je retiens en particulier :
$\dfrac{BI}{BA}=\dfrac{IJ}{AC}$ (1)
Puisque $AI=x$, $AB=a$ et $I\in[AB]$, alors $BI= a-x$
Quant à AC c'est la longueur de la diagonale du carré de côté $a$..
Soit tu sais par cœur (pas besoin de le démontrer) que $AC=a\sqrt 2$ (de même, tu pourrais savoir par cœur que la hauteur d'un triangle équilatéral de côté a mesure $\dfrac{a\sqrt 3}{2}$)
Soit tu le redémontres :
$AB= BC = a$ ce sont les côtés du carré
et puisque l'angle $\hat B$ est droit, le triangle ABC est rectangle en B.
Avec le th de Pythagore :
$AC^2=AB^2+BC^=a^2+a^2=2a^2$ D'où $AC =a\sqrt 2$
Je remplace BI, BA et AC dans (1) :
$\dfrac{a-x}{a}=\dfrac{IJ}{a\sqrt 2}$ (1)

D'où $IJ=\dfrac{(a-x)\times a\sqrt 2}{a}$ je simplifie par a : (non nul sinon, il n'y aurait ni carré, ni exercice)
$IJ=\cdots$

Je te laisse poursuivre...

@+

yannD · 05-01-2020 21:29:02

Bonsoir Yoshi, merci pour ta réponse...
calcul de IJ
On sait que le triangle AIL est rectangle isocèle, donc d'après le théorème de Pythagore :
$AI^2+AL^2=IL^2 $
d'où : $IL^2 = x^2+x^2$
$IL^2 = 2x^2$
$Il^2 = \sqrt{2x^2}$
$IL = \sqrt{2}+\sqrt{x^2}$
$IL = x\sqrt{2}$
calcul de IL

dans le triangle rectangle isocèle BIJ, le théorème de Pythagore, nous donne :
$BI^2+BJ^2=IJ^2$
d'où : $IJ^2 = (a-x)^2+(a-x)^2$
$IJ^2 = 2(a-x)^2$
$ IJ= \sqrt{2(a-x)^2}$
$IJ = \sqrt{2} +\sqrt{(a-x)^2}$
$IJ = \sqrt{2}(a-x)$

aire du rectangle I J K L
$IJ \times IL = x\sqrt{2}\times (a-x)\sqrt{2}$

yoshi · 05-01-2020 21:44:17

RE,

Termine l'affichage, s'il te plaît...
Ayant bien mis en évidence la formule donnant l'aire en fonction de a et x, il te reste les questions d) et e)...
Là, ça devrait être de la routine, quoi...
Raison de plus pour ouvrir l'oeil, s'pas... Il est quand ton DS ?

@+

yannD · 05-01-2020 21:52:23

le DS, c'est mardi

yannD · 05-01-2020 21:54:11

$x\sqrt{2}\times (a-x)\sqrt{2}= ??????$

yoshi · 05-01-2020 22:16:08

Re,

Décomposons :
$x\sqrt{2}\times (a-x)\sqrt{2}=x\times \sqrt 2\times (x-2)\times \sqrt 2 = (\sqrt 2\times \sqrt 2) \times x(x-2)=\cdots$

▼Texte caché

Au pire, celui qui ne sait pas répondre à c) doit jouer franc-jeu et écrire sur sa copie pour le c) :
Je n'arrive pas à trouver l'aire, donc j'admets le résultat et je fais les deux questions suivantes.
Ces deux questions si elles sont bonnes seront comptées justes sans pénalité...

@+

yannD · 05-01-2020 22:17:54

j'ai fait la méthode avec Thalès

dans le triangle ABD ,
$\dfrac{AI}{AB}=\dfrac{AL}{AB}=\dfrac{IL}{AC}$
et en particulier
$\dfrac{AI}{AB}=\dfrac{IL}{AC}$

Puisque le triangle est rectangle, on sait que $AC = a\sqrt{2}$
Ainsi en remplaçant $AI$ par x, et $AB$ par a, on obtient :
$\dfrac{AI}{AB}=\dfrac{IL}{AC} <=> \dfrac{x}{a}=\dfrac{IJ}{a\sqrt{2}}<=> IJ = \dfrac{x}{a}\times a\sqrt{2} = x\sqrt{2}$

dans le triangle ABC :
$\dfrac{BI}{BA}=\dfrac{BJ}{BC}=\dfrac{IJ}{AC}$

et en particulier $\dfrac{BI}{BA}=\dfrac{IJ}{AC}$

puisque I est un point de [AB] alors $BI = (a-x)$

$\dfrac{(a-x)}{a}=\dfrac{IJ}{a\sqrt{2}}$

d'où $IJ = \dfrac{a\sqrt{2}\times(a-x)}{a} = \sqrt{2}(a-x)$

pour la c) j'ai mis $x\sqrt{2}\times (a-x)\sqrt{2}=\dfrac{1}{2} \times a^2$ puisque l'aire d'un carre de côté a est $a^2$ alors la moitié de son aire est $\dfrac{1}{2}\times a^2$

Dernière modification par yannD (05-01-2020 22:27:54)

yoshi · 05-01-2020 22:42:04

Re,

Oui, pour Thalès : il y avait des triangles et des parallèles, donc j'ai tout de suite pensé à Thalès...
Yann, m'enfin...
$x\sqrt{2}\times (a-x)\sqrt{2}=x\times \sqrt 2\times (x-2)\times \sqrt 2 = (\sqrt 2\times \sqrt 2) \times x(x-2)=\cdots$
Que vaut $\sqrt 2 \times \sqrt 2$ ?

Définition : on appelle racine carrée de a positif ou nul le nombre b tel que son carré soit égal au nombre a.
$\sqrt 2 \times \sqrt 2 =(\cdots)^2=\cdots$

Alors, ça y est cette fois ?

Pour d) oui $\cdots= \dfrac{a^2}{2}$
Pour e) ce n'est plus la moitié mais le tiers...

@+

yoshi · 05-01-2020 22:55:26

$4a-4ax^2-a^2=0$

Non, développement incorrect...

$4x(a-x)=a^2$
C'est $4x$ que tu distribues sur $a$, puis sur $-x$

@+

yannD · 05-01-2020 22:58:54

oui, j'ai supprimé le message , j'ai voulu le modifier
$4x(a-x)=a^2$
$4ax-4x^2=a^2$
$4ax-4x^2-a^2=0$
$4x^2-4ax+a^2=0$

$\Delta = (-4)^2-4(4)= $

Dernière modification par yannD (05-01-2020 23:01:33)

yannD · 05-01-2020 23:02:26

je te dit bonne nuit... il faut que j'aille dormir
merci pour ton aide

yoshi · 05-01-2020 23:13:14

Re,

Bien.
Maintenant, résolution équation du 2nd degré...
Ton calcul de $\Delta$ est faux...
* Le coefficient de $x^2$ est bien 4
Mais
le $b$ de $ax^2+bx+c$ ce n'est pas ici -4. Non, le coefficient de $x$ n'est pas -4.
Quant au $c$, ce n'est pas 1...
Quand le coefficient contient a, tu dois garder a...
$4$$x^2$$-4a$$x$$+a^2$=0$

▼1 seule solution

Question e)
2 solutions symétriques par rapport à 3
On remplace a par 6 dans l'équation :
$2x(a-x)=\dfrac{a^2}{3}$

▼Voilà les calculs :

Maintenant, c'est mon tour d'aller me jeter dans les bras de Morphée...

@+

yannD · 06-01-2020 07:54:36

▼Texte caché

yoshi · 06-01-2020 10:29:26

Bonjour,

Tu te lèves tôt...
Tiens en parlant Polynômes, pendant que tu te débattais avec le sieur Zebulon, je suis tombé sur le sujet posté une demoiselle en détresse qui concernait un exo de son DM, en forme de QCM, qie j'ai parfois légèrement modifiées à ton intention.

Dire si les affirmations suivantes sont vraies ou fausses et pourquoi :
1. Pour tout réel $x$, on a : $9x^2-6x+1>0$.
2. Quel que soit le réel donné $a$ non nul, l'équation $x^2+ax+a^2=0$ d'inconnue $x$ n'a pas de solution.
3. La fonction f définie sur $\mathbb R$ par $f(x)=-2x^2+8x-1$ a pour minimum 7.
4. L''équation $x^2+x-1-\sqrt{a^2}=0$, où a est un réel donné, possède deux racines dont le produit est $-1$.
5. Si on note $ x_1$ et $x_2$ les deux racines de l'équation $ax²+bx+c=0$ alors $\dfrac{1}{x_1} + \dfrac{1}{x_2}= -\dfrac b c$.

Si tu t'en sens encore le courage...

Voilà pourquoi, j'ai demandé quand était ton DM.

@+

yannD · 06-01-2020 14:16:09

Bonjour, ce n'est pas un DM mais un DS, et il faut que je me lève tôt pour prendre mon bus;

1. Pour tout réel x, on a $9x²-6x+1 >0$
je dois chercher les valeurs pour lesquelles la parabole est au dessus de l'axe des abscisses, pour cela je calcule le discriminant : $\Delta = b²-4ac = (-6)²+4\times 9 \times 1 = 36 - 36 = 0$
donc pour ce polynôme, j'ai trouvé un delta qui est nul et si $\Delta = 0$, il y a une solution double b/2a

J'ai un doute et je suis en train de me demander comment on trouve une solution double .. quand je suis arrivé à : $f(x) = a (x+b/2a)² -( b²-4ac/4a²)$, comme j'ai trouvé b²-4ac = 0 , j'ai une fraction 0/4a²
et l'équation à résoudre revient à écrire : (x - b/2a)² = 0 et c'est ici où je ne vois plus comment je trouve les 2 solutions
mais pour cette question, je réponds que c'est oui, (tu n'as pas demandé de justifier

Dernière modification par yannD (06-01-2020 14:43:49)

yannD · 06-01-2020 14:51:00

(x+b/2a)²= 0 <=> (x+b/2a)(x+b/2a) = 0

yoshi · 06-01-2020 16:12:57

Re,

Bin, tu trouves une solution double lorsque
* Avec la forme canonique tu as ce qui suit le carré qui est nul, c'est à dire $\dfrac{b^2-4c}{4a^2}=0$ ou encore [tex]b^2-4ac =0[/tex]
* En calculant le discriminant, lorsque celui-ci est nul...
Là tu vas me dire : c'est la même chose puisque $\Delta=b^2-4ac$...
Bin oui, parce que lorsqu'on a écrit $ax^2+bx+c=a\left[\left(x+\dfrac{b}{2a}\right)^2 -\dfrac{b^2-4c}{4a^2}\right]$ , c'est justement là, qu'on a décidé d'utiliser directement à partir de $ax^2+bx+c$, sans passer par la forme canonique, la quantité au numérateur $b^2-4c$ et de l'appeler discriminant avec comme symbole $\Delta$.
Si $\Delta<0$ pas de solution
Si $\Delta=0$ une solution double parce qu'alors $ax^2+bx+c=a\left(x+\dfrac{b}{2a}\right)^2$ et oui : $a\left(x+\dfrac{b}{2a}\right)^2=a\left(x+\dfrac{b}{2a}\right)\left(x+\dfrac{b}{2a}\right)$
Solution(s) $x=-\dfrac{b}{2a}$, et non $x_1=x_2=\dfrac{b}{2a}$ comme tu l'as écrit... ;-)
Dans le cas particulier de cet exercice, ton discriminant te prouve que tu aurais dû voir le produit remarquable $a^2-2ab+b^2=(a-b)^2$.
En effet, $9x^2-6x+1 = (3x)^2-2\times 3x \times 1+1^2=(3x-1)^2$...
C'était plus rapide, moins fatigant...
La question posée devient Est-il (toujours) vrai que $(3x-1)^2>0$.
Toi, tu réponds oui, et je te comprends, tu as en tête : un carré est toujours positif et vous en avez parlé avec Zeb, je n'ai rien dit...
Pourtant la formulation exacte est : un carré est toujours positif ou nul.
Là la bonne réponse est en réalité $(3x-1)^2 \geqslant 0$.
Donc puisque $>0$ et $\geqslant 0$,ce n'est pas tout à fait pareil, je répondrais Non à la question, en précisant $(3x-1)^2 \geqslant 0$...

@+

yannD · 06-01-2020 18:42:06

Bonsoir Yoshi,

on a : $ax^2+bx+x = a\left[\left(x+\dfrac{b}{2a}\right)^2 -\dfrac{b^2-4ac}{4a^2}\right]$

la quantité au numérateur : $b^2 - 4ac$ s'appelle $\Delta$

Maintenant, si $\Delta = 0$ , on a : $a\left[\left(x+\dfrac{b}{2a}\right)^2 - \dfrac{0}{4a^2}\right]$

et la fraction $\dfrac{0}{4a^2}$, je peux dire qu' elle est nul ?? c'est ça ?

yoshi · 06-01-2020 18:54:37

Ave,

Bien rentré ?

Oui bien sûr... La fraction $\frac a b$ c'est l'écriture du quotient exact de a par b...
Alors qu'est-ce-que le quotient exact de $0$ par $4a^2$, sinon $0$ ?
Oui, $\dfrac{0}{4a^2}=0$ , pourquoi ce doute subitement ?

Es-tu allé au bout de la préparation à ton DS que tu nous avais proposé ? as-tu obtenu les mêmes résultats que ceux mis en spoiler ?

@+

yannD · 06-01-2020 19:19:09

on a : $a\left[ \left( x+\dfrac{b}{2a} \right)^2 - \dfrac{0}{4a^2}\right]$ donc je peux écrire : $a\left[ \left(x+\dfrac{b}{2a}\right)^2 - 0 \right]$

Forum de mathématiques - Bibm@th.net

#1 05-01-2020 12:47:33

Révision polynômes

#2 05-01-2020 15:51:45

Re : Révision polynômes

#3 05-01-2020 16:04:38

Re : Révision polynômes

#4 05-01-2020 16:05:58

Re : Révision polynômes

#5 05-01-2020 16:11:46

Re : Révision polynômes

#6 05-01-2020 19:50:25

Re : Révision polynômes

#7 05-01-2020 21:29:02

Re : Révision polynômes

#8 05-01-2020 21:44:17

Re : Révision polynômes

#9 05-01-2020 21:52:23

Re : Révision polynômes

#10 05-01-2020 21:54:11

Re : Révision polynômes

#11 05-01-2020 22:16:08

Re : Révision polynômes

#12 05-01-2020 22:17:54

Re : Révision polynômes

#13 05-01-2020 22:42:04

Re : Révision polynômes

#14 05-01-2020 22:55:26

Re : Révision polynômes

#15 05-01-2020 22:58:54

Re : Révision polynômes

#16 05-01-2020 23:02:26

Re : Révision polynômes

#17 05-01-2020 23:13:14

Re : Révision polynômes

#18 06-01-2020 07:54:36

Re : Révision polynômes

#19 06-01-2020 10:29:26

Re : Révision polynômes

#20 06-01-2020 14:16:09

Re : Révision polynômes

#21 06-01-2020 14:51:00

Re : Révision polynômes

#22 06-01-2020 16:12:57

Re : Révision polynômes

#23 06-01-2020 18:42:06

Re : Révision polynômes

#24 06-01-2020 18:54:37

Re : Révision polynômes

#25 06-01-2020 19:19:09

Re : Révision polynômes

Pied de page des forums